⭐文章目录⭐
👇
External Sorting
Introduction
When data are too large to fit into internel memory, external sorting is a technique to sort them. It involves dividing the data into smaller chunks, sorting each chunk independently, and then merging the sorted chunks to obtain the final sorted result.
Examples
Defination
- $B$ is the fixed-size of a block of data that can be read from the external storage.
- $M$ is the number of blocks that the internal memory can solve once at a time.
- $p$ is the number of passes needed to sort the data.
- $b$ is the total I/O cost, which equals to the number of blocks.
Now we have a internal memory with $M=3,B=1$.
And the data with size $N=13$ is originally stored in a tape $T_1$ in the external storage.
2-way merge algorithm

- step 1: We first load in the first three blocks of $T_1$ into the internal memory and sort them.
- step 2: Then we write the sorted data (a run) back to a new tape $T_2$.
- step 3: We load the second three blocks of $T_1$ into the internal memory and sort them.
- We write the sorted data back to a new tape $T_3$.
- step 4: We repeat step 2 and 3 for the remaining blocks of $T_1$ and then regard $T_1$ as empty.
- step 5: We merge and sort the first pair of run in $T_2$ and $T_3$ and write it back to the empty tape $T_1$.
- step 6: We merge and sort the second pair of run in $T_2$ and $T_3$ and write it back to the a new tape $T_4$.
- step 7: We repeat step 5 and 6 for the remaining pairs of runs in $T_2$ and $T_3$ and then regard $T_2$ and $T_3$ as empty.
- step 8: We repeat step 5 , 6 and 7 until all the data are sorted and stored in a single tape $T$.
The number of runs after step 4 is $r=\lceil\frac{N}{M}\rceil=5$.
The number of operations that merge two tapes is $t=\lceil\log_2\lceil\frac{N}{M}\rceil\rceil=3$.
The number of passes is $p=1+t=4$.
The cost of I/O is $b=2\frac{N}{B}\times p=104$.
What we concern are
- seek time (number of passes)
- time to merge $N$ records from input buffers to the output buffer
- time to internally sort $M$ records
- time to read or write one block of records
So our goal is to - minimize the number of passes
- minimize the number of run merges
- minimize the number of run generation
- minimize the number of buffer handling for parallel operation
Reduce number of passes
Use a $k$-way merge algorithm to merge the runs in parallel.
So the number of passes $p=1+\lceil\log_k\lceil\frac{N}{M}\rceil\rceil$.
It do decrease the number of passes, but since this algorithm requires $2k$ tapes, it is not good enough.
Reduce the number of tapes
Try to use 3 tapes to solve 2-way merge problem.
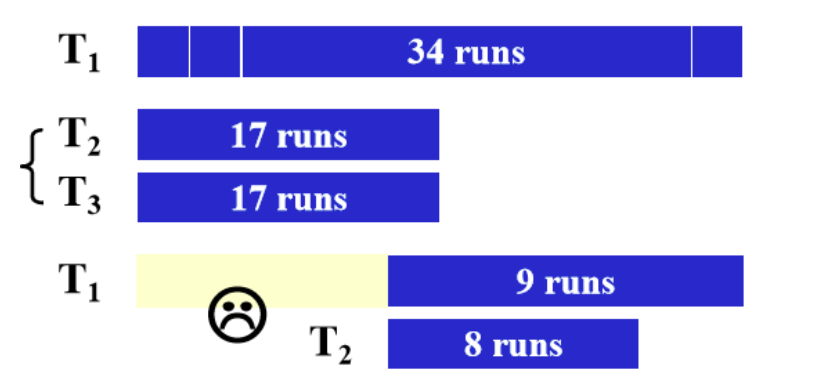
If we simply use the old way, we may stuck here.
So, if we are given two tapes with number of runs $r_2=5$ and $r_3=3$,
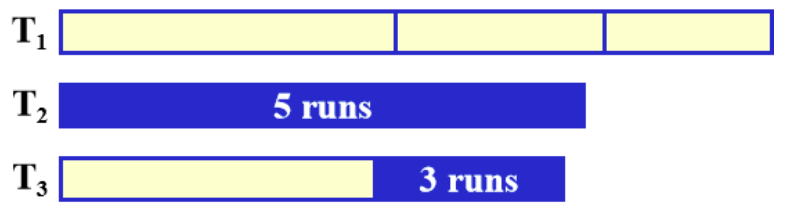
rather than put the even pairs and odd pairs into two tapes respectively, we can put the first 3 pairs into an empty tape $T_1$ and do nothing to the remained 2 runs.

With this strategy, we can reduce the number of tapes from $2k$ to $k+1$.
If we review the processure of 2-way merge in reverse order,we can find that the number of runs in the longest tape is:
$$F_0=0,F_1=1,F_2=1,F_3=2,F_4=3\cdots F_N=F_{N-1}+F_{n-2}$$
It is a Fibonacci sequence!!
So we can do our best to assign the number of runs in each tape to the Fibonacci sequence.
It also has a similar property in k-way merge algorithm,that is:
$$F_{N}^k=\begin{cases}0,\quad 0\leq N\leq k-2\\1,\quad N=k-1\\\sum_{i=1}^{k}F_{N-i}^k,\quad N\geq k\end{cases}$$
Handle the buffers for parallel operation
- Buffer: When we are doing parallel writing and reading, we need to store both input and output data in the buffer.
When the $k$ rises, the number of input buffers will increase,the size of buffer will decrease,the size of block will decrease,which end up with increasing the seeking time.
In general, for a $k$-way merge we need $2k$ input buffers and $2$ output buffers for parallel operations.
Beyond a certain $k$ value, the I\O time would actually increase despite the decrease in the number of passes being made. The optimal value for $k$ clearly depends on disk parameters and the amount of internal memory available for buffers.
Can we get a longer run each time?
Yes,apart from selecting $M$ elements and sort then, we can do as follows:
- step 1: Select first $M$ elements and sort them.
- step 2: Write the lowest one to the tape.
- step 3: Add the next element to the remained $M-1$ elements and sort them.
- step 4: Write the lowest one of those who are not greater than the previous one to the tape.
- step 5: Repeat until there is no element left or all the $M$ elements in the buffer are greater than the previous one.Then one tape is built.
- step 6: Repeat step 1 to step 5 for the remaining elements to build more runs.
It is proved that the average length of a run $L_{avg}=2M$.
How to minimize merging time?
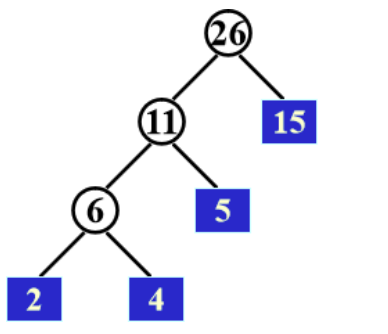
We can use a Huffman Tree to minimize the number of merging times.
For example,we are given 4 runs with length $l_1=2,l_2=4,l_3=5,l_4=15$.The best sequence to merge them is in the following order: