⭐文章目录⭐
👇
Parallel Algorithms
Definition
To describe a parallel algorithm, we need to define the following terms:
- Parallel Random Access Machine (PRAM): a parallel machine that can perform random access operations, such as reading and writing memory locations.
- Work-Depth
Parallel Random Access Machine
for i from 1 to n pardo
A[i] = B[i] (read / write in a unit time)
As we read in a shared memory system in the same time, we may encounter conflicts.
To resolve access conflicts
- 1.Exclusive Reading Exclusive Writing (EREW)
- 2.Concurrent Reading Exclusive Writing (CREW)
- 3.Concurrent Reading Concurrent Writing (CRCW)
- This may need to define a rule for access.
- Arbitrary rule
- Priority rule
- Common rule
- This may need to define a rule for access.
Work-Load and Work-Depth
- Work-Load $W(n)$: total amount of work/operations needed to complete the algorithm.
- Work-Depth $T(n)$: worst-case running time of the algorithm.There are some asymptotically equivalent definitions of work-depth and work-load:
- $P(n) = W(n)/T(n)$ processors and $T(n)$ time (on a PRAM)
- $W(n)/p$ time using any number of $p ≤ W(n)/T(n)$ processors (on a PRAM).
- $W(n)/p + T(n)$ time using any number of $p$ processors (on a PRAM).
Examples
Summation Problem
Description
Given $n$ numbers and try to compute their sum.
Serial Algorithm
sum = 0
for i from 1 to n
sum = sum + A[i]
It takes $O(n)$ time and the workload is $O(n)$.
Parallel Algorithm
We construct a parallel summation tree like this:
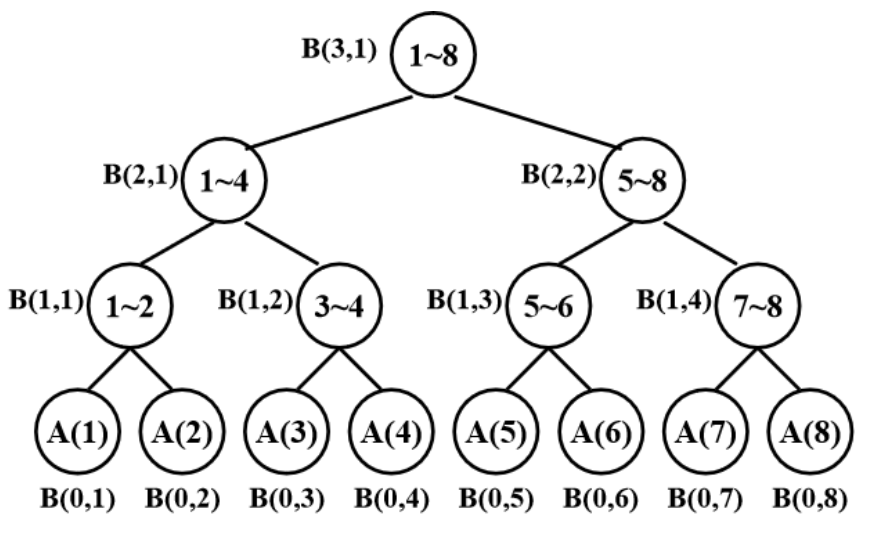
sum = 0
for i from 1 to n pardo
B(0,i)=A(i)
for i from 1 to log n:
for j from 1 to n/2^i pardo
B(i,j)=B(i-1,2*j-1)+B(i-1,2*j)
$T_P(n)$=running time with p CPU.
$T_1(n)=O(n)$,which is called the Work-Load $W(n)$
$T_\infty(n)=O(\log n)$,which is called the Work-Depth $T(n)$.
$T_P(n)$ for an arbitrary $p$:$$T_P(n)\geq T(n)$$$$T_P(n)\geq \frac{W(n)}{p}\geq \frac{1}{2}(T(n)+\frac{W(n)}{p})$$
Prefix Sum Problem
Description
Given $n$ numbers and try to compute their prefix sum $S={\sum_{i=1}^{k}a_i,for\ k\ from\ 1\ to\ n }$.
Serial Algorithm
$W(n)=O(n)$, $T(n)=O(n)$
Parallel Algorithm
Naive Parallel Algorithm
Parallelly compute the sum of each subarray by using parallel summation tree.
$W(n)=O(1+2+\cdots+n)=O(n^2)$, $T(n)=O(\log n)$
Efficient Parallel Algorithm
We can use the parallel summation tree and improve it in this way.
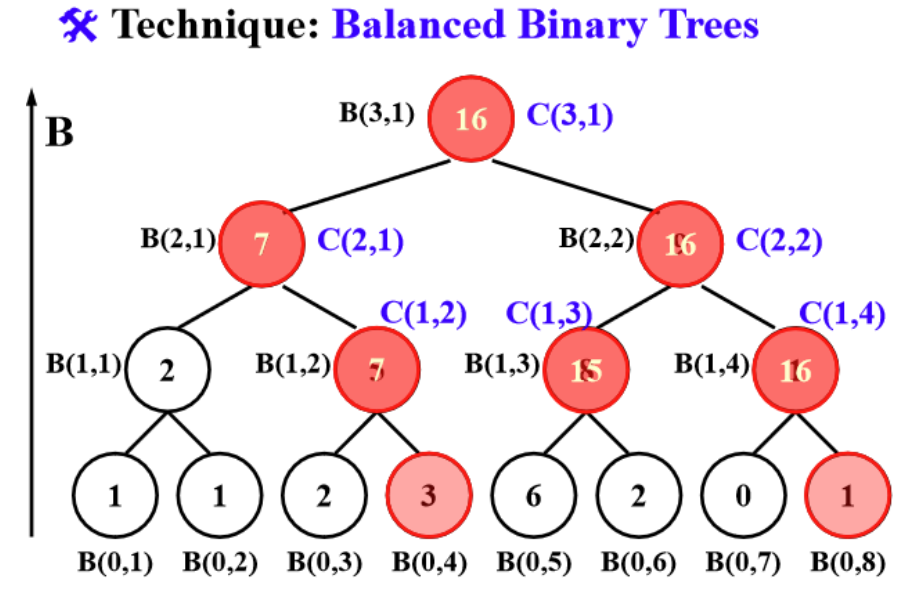
In this tree, we define $$C(h,i)=\sum_{j=1}^{\alpha}A_j$$where $A(\alpha)$ is the rightest leaf of the subtree rooted at $C(h,i)$
For all the $h$, $$C(h,1)=B(h,1)$$
If $C(h,i)$ is a right child,$$C(h,i)=C(h+1,i/2)$$
If $C(h,i)$ is a left child and $i\neq 1$,$$C(h,i)=C(h+1,i/2)-B(h,i+1)=C(h+1,(i-1)/2)+B(h,i)$$
for P_i , i from 1 to n pardo
B(0, i) := A(i)
for h = 1 to log n
for i from 1 to n/2^h pardo
B(h, i) := B(h - 1, 2i - 1) + B(h - 1, 2i)
for h = log n to 0
for i even, i from 1 to n/2^h pardo
C(h, i) := C(h + 1, i/2)
for i = 1 pardo
C(h, 1) := B(h, 1)
for i odd, from 3 to n/2^h pardo
C(h, i) := C(h + 1, (i - 1)/2) + B(h, i)
for P_i , from 1 to n pardo
Output C(0, i)
$W(n)=O(n)$, $T(n)=O(\log n)$
Parallel Merge Sort
Serial Algorithm
sort(A):
if length(A) <= 1:
return A
else:
B=left_half(A)
C=right_half(A)
D=sort(B)
E=sort(C)
return merge_sort(D,E)
| W | P | |
|---|---|---|
| divide | $O(1)$ | $O(1)$ |
| conquer | $2W(n/2)$ | $O(n/2)$ |
| merge | $O(n)$ | $O(n)$ |
$W(n)=O(n\log n)$, $T(n)=O(n)$
Parallel Algorithm
If we define the $rank(i,A)$ as the rank of $A[i]$ in $B$ and $rank(i,B)$ as the rank of $B[i]$ in $A$, for the merge operation, we can use the following algorithm:
for i from 1 to n pardo:
C[i+rank(i,B)]=A[i]
C[j+rank(j,A)]=B[j]
$W(n)=O(n)$, $T(n)=O(1)$
Then we have the subproblem:
Ranking Problem
Serial Algorithm
Do like what merge does.
$W(n)=O(n)$, $T(n)=O(n)$
It does not safe any time.
Binary Search Algorithm
We use binary search to find the rank of each element in the other array.
for P_i , i from 1 to n pardo:
RANK(i, B) := BS(A(i), B)
RANK(i, A) := BS(B(i), A)
$W(n)=O(n\log n)$, $T(n)=O(\log n)$
Parallel Ranking Algorithm
Assume that $n = m$ ; and that $A(n+1)$ and $B(n+1)$ are each larger than both $A(n)$ and $B(n)$.
for i from 1 to n / k pardo :
rank(i*k + 1, A) := BS(A(i*k + 1), A(n+1))
rank(i*k + 1, B) := BS(B(i*k + 1), B(n+1))
In this step,
$W_1(n)=O(\frac{n\log n}{k})$, $P_1(n)=O(\log n)$
Then we have will have:
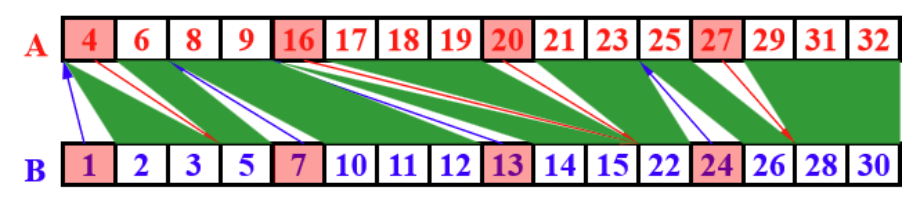
What we need to do is to compute the rank of each element locally in the subarray.
In this step,
$W_2(n)=O(n)$, $P_2(n)=O(k)$
We set $k$ as $\log n$,then we can compute the total workload and work-depth as:
$W(n)=O(n)$, $T(n)=O(\log n)$
Under this method,
| W | P | |
|---|---|---|
| divide | $O(1)$ | $O(1)$ |
| conquer | $2W(n/2)$ | $O(n/2)$ |
| merge | $O(n)$ | $O(\log n)$ |
$D(n)=O((\log n)^2)$
Maximum Finding Problem
Description
Given $n$ numbers and try to find the maximum number.
Serial Algorithm
$W(n)=O(n)$, $T(n)=O(n)$
Binary Search Algorithm
$W(n)=O(n)$, $T(n)=O(\log n)$
Comparing All Pairs
for i from 1 to n pardo:
B[i]=0
for every pair (i,j) 1 <= i <= j pardo:
if A[i] < A[j]:
B[i]=0
if A[i] > A[j]:
B[j]=0
for i from 0 to n pardo:
if B[i]==0:
return A[i]
$W(n)=O(n^2)$, $T(n)=O(1)$
Doubly-logarithmic Paradigm
1.Divide the array into $\sqrt{n}$ parts.
2.Recursively find the maximum of each part.
3.Find the maximum of the $\sqrt{n}$ maximums.
$$\begin{cases}W(n)=\sqrt{n}W(\sqrt{n})+O(n)\\W(1)=O(1)\end{cases}\rightarrow W(n)=O(n\log \log n)$$$$\begin{cases}T(n)=T(\sqrt{n})+O(1)\\T(1)=O(1)\end{cases}\rightarrow T(n)=O(\log \log n)$$
If we partition the array into $k$ parts, then we can use the same algorithm recursively on each part.
$W(n)=O(n+k\log\log k)$, $T(n)=O(\frac{n}{k}+\log\log k)$
Let $k=\frac{n}{\log\log n}$, then we have:
$W(n)=O(n)$, $T(n)=O(\log\log n)$
Random Sampling Algorithm
This algorithm can reach
$W(n)=O(n)$, $T(n)=O(1)$ with success probability $1-\frac{1}{n^c}$,in which $c$ is a constant.
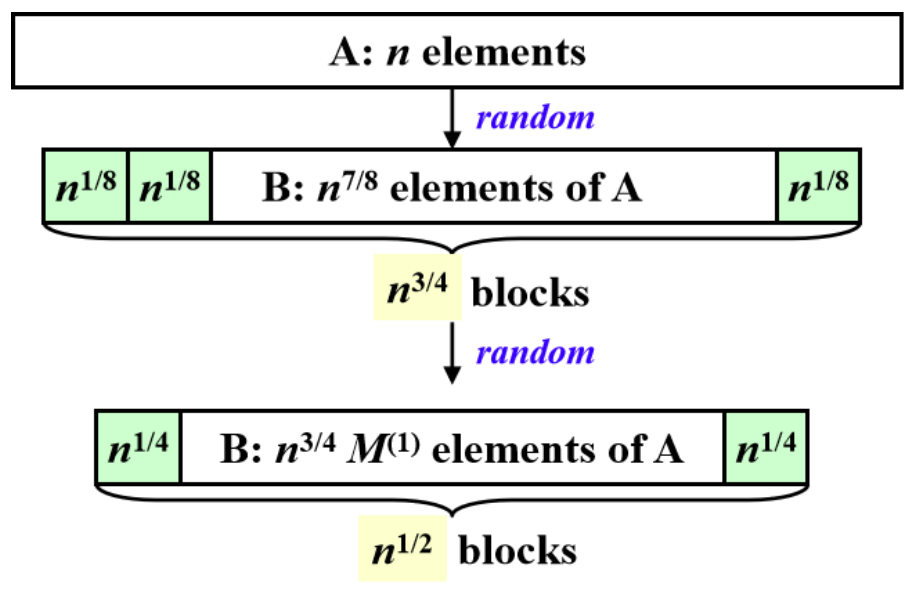
Steps are as follows:
- 1.Randomly select $n^\frac{7}{8}$ elements from the array (It has a high probability that the maximum is in this set).
- 2.Divide the set into $n^\frac{3}{4}$ parts,each with size $n^\frac{1}{8}$.
- 3.Solve each part by Comparing All Pairs algorithm parallelly.
- This step has $W(n)=O( (n^\frac{1}{8})^2)=O(n^\frac{1}{4})=O(n)$, $T(n)=O(1)$.
- 4.Then we have a set with size $n^\frac{3}{4}$ and each element is the maximum of its corresponding part.
- 5.Divide the set into $n^\frac{1}{2}$ parts,each with size $n^\frac{1}{4}$.
- 6.Solve each part by Comparing All Pairs algorithm parallelly.
- This step has $W(n)=O( (n^\frac{1}{4})^2)=O(n^\frac{1}{2})=O(n)$, $T(n)=O(1)$.
- 7.Then we have a set with size $n^\frac{1}{2}$ and each element is the maximum of its corresponding part.
- 8.Find the maximum of the $n^\frac{1}{2}$ maximums by comparing all pairs.
- This step has $W(n)=O((n^\frac{1}{2})^2)=O(n)$, $T(n)=O(1)$.
So the $W_{total}(n)=O(n), T_{total}(n)=O(1)$
