⭐文章目录⭐
👇
Local Search
Definition
- Local
- Define neighborhoods in the feasible set
- A local optimum is a best solution in a neighborhood
- Search
- Start with a feasible solution and search a better one within the neighborhood
- A local optimum is achieved if no improvement is possible
SolutionType Gradient_descent()
{ Start from a feasible solution S in FS ;
MinCost = cost(S);
while (1) {
S’ = Search( Negihbor(S) ); /* find the best S’ in Neighbor(S) */
CurrentCost = cost(S’);
if ( CurrentCost < MinCost ) {
MinCost = CurrentCost; S = S’;
}
else break;
}
return S;
}
Vertex Cover Problem
Definition
Give a Graph $G=(V,E)$, a vertex cover is a subset $C$ of $V$ such that for every edge $(u,v)\in E$, either $u\in C$ or $v\in C$.
Gradient_descent Algorithm
We deine:
- $FS=${$s\subseteq V $|$s$ is a vertex cover }.
- $cost(s)=|S|$
- $N(s)=${$s’$|$s’$ is a vertex cover and $s’ \subset s$ or $s \subset s’$ and $||s’|-|s||=1$}.
LSVC(V,E):
s=V
while (true){
if s-{u} is a vertex cover for a u in V:
s=s-{u}
else:
return s
}
But we can find in the case that picture below has shown:
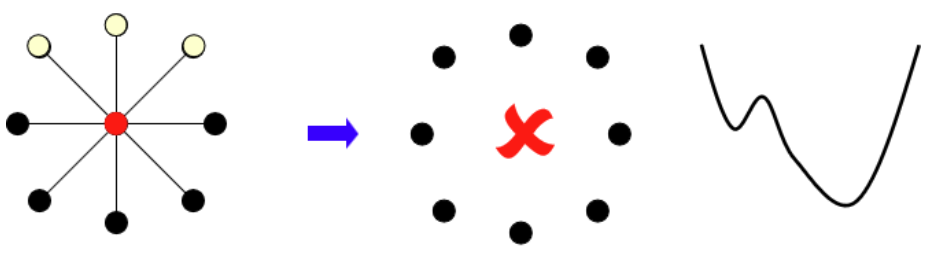
The Gradient_descent algorithm may not work well in this case.
So we need to improve.
Metropolis Algorithm
SolutionType Metropolis()
{ Define constants k and T;
Start from a feasible solution S in FS ;
MinCost = cost(S);
while (1) {
S’ = Randomly chosen from N(S);
CurrentCost = cost(S’);
if ( CurrentCost < MinCost ) {
MinCost = CurrentCost; S = S’;
}
else {
With a probability p, let S = S’;
else break;
}
}
return S;
}
In this algorithm,we define:
- $p=e^{\frac{-\Delta cost}{KT}}$
- $\Delta cost=cost(S’)-cost(S)$
Simulate Annealing Algorithm
Gradually decrease $T$ in the Metropolis Algorithm to avoid getting stuck in local optima.
Hopfield Neural Network Problem
Description
- Given a Graph $G=(V,E)$ with edge weights.
- We define each vertex has a state $s\in \lbrace0,1}$.
- $e$ is a good edge if $w_es_us_v<0$
Our goal is to find a configuration $S$ maximize $\sum_{e\ is\ good}{|w_e|}$
State Flipping Algorithm
Definition
- In a configuration $S$, a vertex $u$ is satisfied if the weight of incident good edges is large than the weight of incident bad edges,that is $\sum{w_eu_vs_v} \leq 0$.
- A configuration $S$ is stable if all vertex $u$ are satisfied.
Algorithm
ConfigType State_flipping()
{
Start from an arbitrary configuration S;
while ( ! IsStable(S) ) {
u = GetUnsatisfied(S);
flipstate(u);
}
return S;
}
Theorem
- The State Flipping Algorithm terminates at a stable configuration after at most $W = \sum_e|w_e|$ iterations.
Proof:
- Let $\phi(S)=\sum_{e\ is\ good}{|w_e|}$.
- We have: $\phi(S) < \phi(S’) \leq \sum{|w_e|=W}$
- And each flip increse $\phi(S)$ by at least 1.
- So it takes less than $W$ flips.
Max Cut Problem
Description
Given a Graph $G=(V,E)$, a cut is a partition of $V$ into two sets $A$ and $B$.
$\delta(A,B)=\lbrace(u,v)|u\in A,v \in B\rbrace$
Our goal is to find a cut that maximize $W(A,B)=\sum_{e\in\delta(A,B)}{w_e}$.
State Flipping Algorithm
Definition
- In a configuration $S$, a vertex $u$ is satisfied if the weight of incident cut edges is large than the weight of incident nun-cut edges,that is $\sum_{cut\ edge} {w_e} < \sum_{non-cut\ edge} {w_e}$.
- A configuration $S$ is stable if all vertex $u$ are satisfied.
- State of a vertex means it is either in set $A$ or set $B$.
ConfigType State_flipping()
{
Start from an arbitrary configuration S;
while ( ! IsStable(S) ) {
u = GetUnsatisfied(S);
su = - su;
}
return S;
}
Lemma
This algorithm is 2-approximation algorithm.
Proof:
for $u \in A$
$$\sum_{cut\ edge} {w_e} \geq \sum_{non-cut\ edge} {w_e}$$ $$\sum_{u\in A}\sum_{cut\ edge} {w_e} \geq \sum_{u\in A}\sum_{non-cut\ edge} {w_e}$$$$W(A,B)\geq2W(A)$$
The same,$$W(A,B)\geq2W(B)$$
So,$$2W(A,B)\geq2W(A)+2W(B)=2W-2W(A,B)$$$$W(A,B)\geq\frac{1}{2}W$$
Big-improvement-flip
Definition
- Flip only when there is a big improvement ($W(A,B)$ increases at least by a factor of $1+\frac{\epsilon}{|V|}$)
Theorem
- Time complexity: $O(\frac{n}{\epsilon}\log W)$
Proof:
$$(1+\frac{\epsilon}{|V|})^t\leq W$$$$t\leq \log_{(1+\frac{\epsilon}{|V|})}W=O(\frac{n}{\epsilon}\log W)$$
- $W(A,B)\geq W_{OPT}(A,B)/(2+\epsilon)$
K-Flip Algorithm
Definition
- Apart from State Flipping, we define neighborhood as: $$N(S)=\lbraceS’|S’\ can\ be\ obtained\ from\ S\ by\ flipping\ k\ states}$$.
K-L heuristic Algorithm
- Step 1: We get a flip in the unmarked vertex as good as we can to obtain a new configuration $S_1$ from $S$ and mark the fliiped vertex.
- …
- Step k: We get a flip in the unmarked vertex as good as we can to obtain a new configuration $S_k$ from $S_{k-1}$.
- Step n: $S_n=\bar{S}$
- And we define $N(S)=\lbraceS_1,\dots,S_n}$.
- We find the best configuration $S$ in $N(S)$,if there is an improvement, select it.Otherwise, algorithm terminates.
Theorem
This algorithm may increase the running time,but it improve the accuracy of the result.
