⭐文章目录⭐
👇
Dynamic Programming
Definition
The main trouble when solving problems using recursion is that the growth of redundant calculations is explosive. So we need to use dynamic programming, recording the recently computed values, to avoid recursive calls.
- 1.Define subproblems
- 2.Find base cases and recurece relation
- 3.Computing the optimal values for all subproblems
- 4.reconstruct the optimal solution from the optimal values of subproblems
Subset Sum
Descriptions
Given a set of integers, find a subset of integers that has a sum equal to a given target value.
Algorithm
- 1.Define subproblems:
- $S(i,t)=\lbrace y|y\leq t and y =a_1x_1+a_2x_2+\cdots+a_ix_i,x_i\in\lbrace 0,1\rbrace$
- 2.Find base cases:
- $S(0,t)=\lbrace 0\rbrace$
- $S(i,0)=\emptyset$
- 3.Recurrence relation:
- $S(i+1,t)=(S(i,t)\cup \lbrace a_{i+1}\rbrace)\cup (S(i,t)+\lbrace a_{i+1}\rbrace)\cap [0,t]$
- 4.Result is the subset of $S(n,t)$ whose sum is equal to $t$.
Complexity Analysis
$T(n)=O(nt)$
Weighted Independent set on Paths
Descriptions
Given a sequence of $v$ and there corresponding weights.We need to find a subset $S$ with the maximum total weight such that no two vertices in $S$ are adjacent.
Algorithm
- 1.Define subproblems:
- $S(i)=$ the total weight optimal solution for $v_1,v_2,v_3,\cdots,v_i$
- 2.Find base cases:
- $S(0)=0$
- $S(1)=w_1$
- 3.Recurrence relation:
- $S(i)=\max\lbrace S(i-1),S(i-2)+w_i\rbrace$
- 4.Result is the subset of $S(n)$ whose total weight is maximum.
- 5.Output:
- if $C[n] \neq C[n-1]$: print($v_n$),n=n-2
- else: n=n-1
Complexity Analysis
$T(n)=O(n)$
Ordering Matrices Multiplication
Descriptions
For three Matrices $M_{a\times b},M_{b\times c},M_{c\times d}$, when we multiply them together,we have two options:
- 1.$(M_{a\times b}\times M_{b\times c}) \times M_{c\times d}$, the total running time is $abc+acd$
- 2.$M_{a\times b}\times (M_{b\times c} \times M_{c\times d})$, the total running time is $bcd+abd$
The problem is: given a sequance of $n$ matrices, find the optimal order to multiply them together to minimize the total running time.
Algorithm
Define $b_i$ as the number of ways to multiply i matrices together.
We have: $b_1=1,b_2=1,b_3=2,b_4=5,\cdots,b_n=\sum_{i=1}^{n-1}b_i\times b_{n-i}$
- 1.Define subproblems:
- $c[i][j]$ is the minimum cost to multiply $M_i$ to $M_j$
- 2.Find base cases:
- $c[i][i]=0$
- 3.Recurrence relation:
- $c[i][j]=\min\lbrace c[i][k]+c[k+1][j]+r_{i-1}\times r_{k}\times r_{j},k \isin [i,j]\rbrace$
- 4.$c[0][n]$ is the optimal cost to multiply all matrices together.
Complexity Analysis
$T(n)=O(n^3)$
Knapsack Problem
Descriptions
Given a set consisting of $N$ items, where the $i$-th item has size $s_i$ and value $v_i$, and a knapsack capacity $c$, The task is to find a subset of items with the maximum total value such that its total size does not exceed the capacity c.
Algorithm
- 1.Define subproblems:
- $v[i][j]$ be the maximum value for the first $i$ items and a knapsack capacity of $j$.
- 2.Find base cases:
- $v[0][j]=0$
- $v[i][0]=0$
- 3.Recurrence relation:
- $v[i][j]=\max\lbrace v[i-1][j],v[i-1][j-s_i]+v_i\rbrace$
- 4.The maximum value for the first $N$ items and a knapsack capacity of $c$ is $v[N][c]$.
Complexity Analysis
$T(n)=O(nc)$
Optimal BST
Descriptions
Given n keys and their corresponding frequencies,we need to find a BST with minimum average search time($\sum_{i=1}^nf_id(i)$).
Algorithm
Define Tree T as follows:
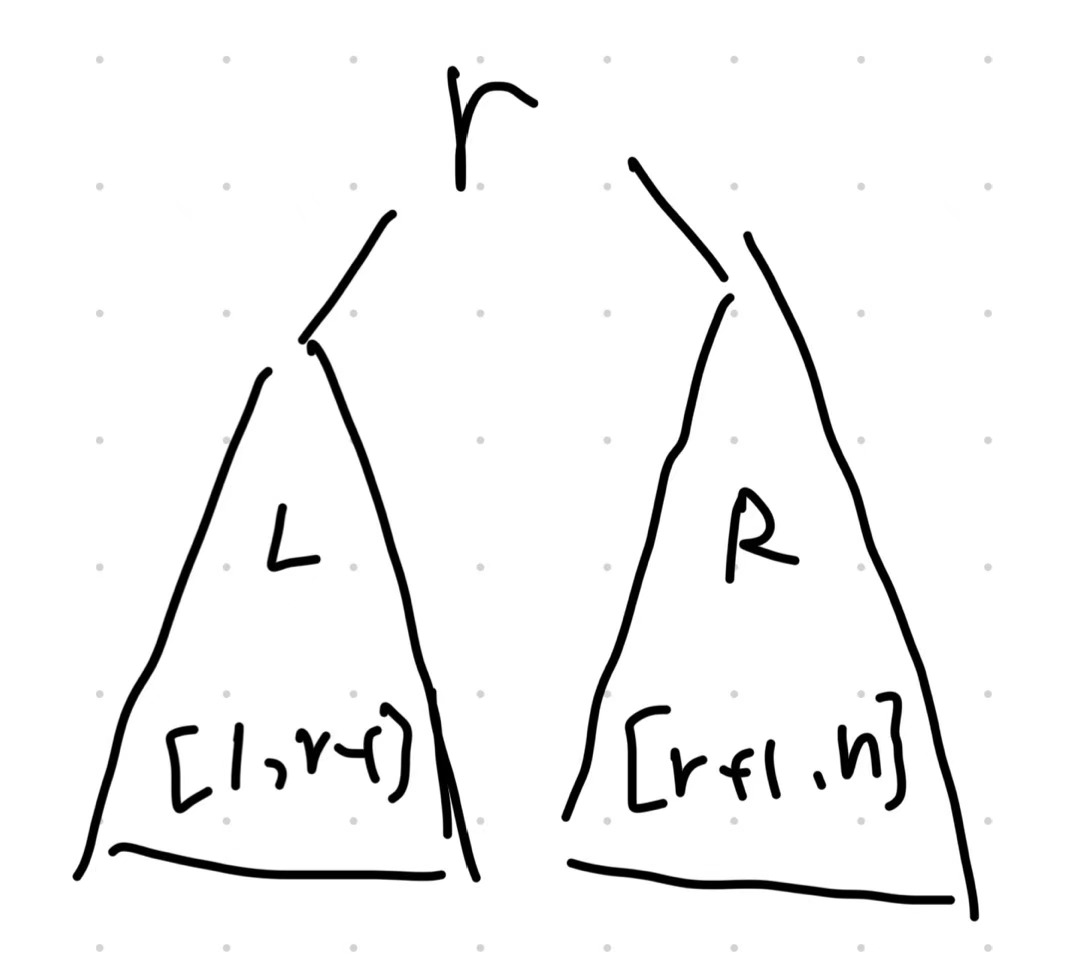
We have:
-
depth of $k$ in T ($k\leq r-1$) = 1 + depth of $k$ in $L$
-
$\sum_{i=1}^nf_id_i^T=\sum_{i=1}^{r-1}f_i(1+d_i^L)+\sum_{i=r+1}^nf_i(1+d_i^R)=\sum_{i=1}^nf_i+\sum_{i=1}^{r-1}f_id_i^L+\sum_{i=r+1}^nf_id_i^R$
-
1.Define subproblems:
- $D[i][j]$ is the average depth of the optimal BST for keys $\in [i,j]$
-
2.Find base cases:
- $D[i][i]=0$
-
3.Recurrence relation:
- $D[i][j]=min_{i\leq r\leq j}\lbrace \sum_{k=i}^jf_i+D[i][r-1]+D[r+1][j]\rbrace$
-
4.The minimum average search time is $\min_{i=1}^nD[1][n]$.
Complexity Analysis
$T(n)=O(n^3)$
Enhanced version
For $D[i][j]$ and $D[i+1][j]$,$r$ and $r’$ are the root of the two subtrees respectively,we have:
- $r \leq r’$
The same,for $D[i][j]$ and $D[i][j-1]$,$r$ and $r’'$ are the root of the two subtrees respectively,we have:
- $r \geq r’'$
Then we can optimize the recurrence relation as follows:
- $D[i][j]=min_{r’‘\leq r\leq r’}\lbrace \sum_{k=i}^jf_i+D[i][r-1]+D[r+1][j]\rbrace$
Complexity Analysis
$T(n)=O(n^2)$
Shortest Path
Descriptions
Given a graph $G=(V,E)$, with edge weights $w_{ij}$, and two vertices $s$ and $t$, we need to find the shortest path from vertex $s$ to vertex $t$.
Algorithm
We can use Dijkstra’s algorithm to solve this problem,which takes $O(|V|\log |V| + |E|)$ time.
But there is also a more efficient algorithm called Bellman-Ford algorithm, which takes $O(VE)$ time.
- 1.Define subproblems:
- $c[v][i]$ is the cost of the shortest path from $s$ to $v$ using at most $i$ edges.
- 2.Find base cases:
- $c[s][0]=0$
- $c[v][0]=+\infty$ for all $v\neq s$
- 3.Recurrence relation:
- $c[v][i]=\min\lbrace c[v][i-1],\min_{u\in E(v)}\lbrace c[u][i-1]+w_{uv}\rbrace$
- 4.The cost of the shortest path from $s$ to $t$ is $c[t][|E|]$.
Lemma
G has no negtive cycles if and only if $c[v][n] == c[v][n-1]$ for all $v\in V$.
All Pairs Shortest Path
Descriptions
Apart from the previous problem, we need to find the shortest path between all pairs of vertices in a graph.
Algorithm
If use single-source algorithms like Dijkstra’s algorithm and Bellman-Ford algorithm to solve this problem, they need to run $|V|$ times,and the time complexity is $O(|V|^2\log |V| + |V||E|)$ and $O(|V|^2|E|)$ respectively.
We can use Floyd-Warshall algorithm to solve this problem, which takes $O(|V|^3)$ time.
For a path $p$, we define $rank(p)$ as the largest index of its internal nodes(exclude the source and destination nodes).
- 1.Define subproblems:
- $c[i][j][k]$ is the cost of the shortest path from $i$ to $j$ with $rank(p)\leq k$.
- 2.Find base cases:
- $c[i][j][0]=\begin{cases}w_e\ \infty \end{cases}$
- 3.Recurrence relation:
- case 1: $rank(p’)\leq k-1$:
- $c[i][j][k]=C[i][j][k-1]$
- case 2: $rank(p’)=k$:
- $c[i][j][k]=c[i][k][k-1]+c[k][j][k-1]$
- $c[i][j][k]=min\lbrace case 1,case 2\rbrace$
- case 1: $rank(p’)\leq k-1$:
- 4.The cost of the shortest path from $i$ to $j$ is $c[i][j][|V|]$.
/* A[ ] contains the adjacency matrix with A[ i ][ i ] = 0 */
/* D[ ] contains the values of the shortest path */
/* N is the number of vertices */
/* A negative cycle exists iff D[ i ][ i ] < 0 */
void AllPairs( TwoDimArray A, TwoDimArray D, int N )
{ int i, j, k;
for ( i = 0; i < N; i++ ) /* Initialize D */
for( j = 0; j < N; j++ )
D[ i ][ j ] = A[ i ][ j ];
for( k = 0; k < N; k++ ) /* add one vertex k into the path */
for( i = 0; i < N; i++ )
for( j = 0; j < N; j++ )
if( D[ i ][ k ] + D[ k ][ j ] < D[ i ][ j ] )
/* Update shortest path */
D[ i ][ j ] = D[ i ][ k ] + D[ k ][ j ];
}
Lemma
G has a negtive cycle if and only if $c[i][i][n]<0$ for some i.
