⭐文章目录⭐
👇
Greedy
Ways of proofment
- Select any solution as the start point.
- Prove that every step does not worsen the solution.
Least Processing Time First (LPT)
Defination:
Given n actitivities, each with a processing time, find a schedule that minimizes the total processing time.
Solution:
Select the least processing time activity each step.
LPT Pro
Defination:
Given n actitivities, each with a start time $s$ and a finish time $f$, find a schedule that maximize the number of activities that can be joined.
Solution:
Select the activity with the earliest finish time each step.
Proof:
$\exist solution S,|S|>|A|$
$A$: optimal solution by Greedy algorithm.
$A=i_1,i_2,…,i_k$
$S=j_1,j_2,…,j_k,j_{k+1},…,j_l$
find the first different activity $i_m$ and $j_m$, we have $f_{im}\leq f_{jm}$.Then $j_m$ can be replaced by $i_m$ to get a better solution.
In the end we have $ S = A + {j_{k+1},…,j_l}$, which not exist in the greedy algorithm.
Prefix Code
Defination:
Given a set of strings $S$,we can code them each with a distinct binary number,like 0,1,10,11.The problem is the given set of strings have a corresponding frequency for each string.We need to find a prefix code that minimizes $\sum_{a\in S}f(a)|c(a)|$, in which $f(a)$ is the frequency of string $a$ and $c(a)$ is the length of the binary code for string $a$.
Solution(Huffman’s algorithm):
We can transform Prefix Code to Binary Tree like this.
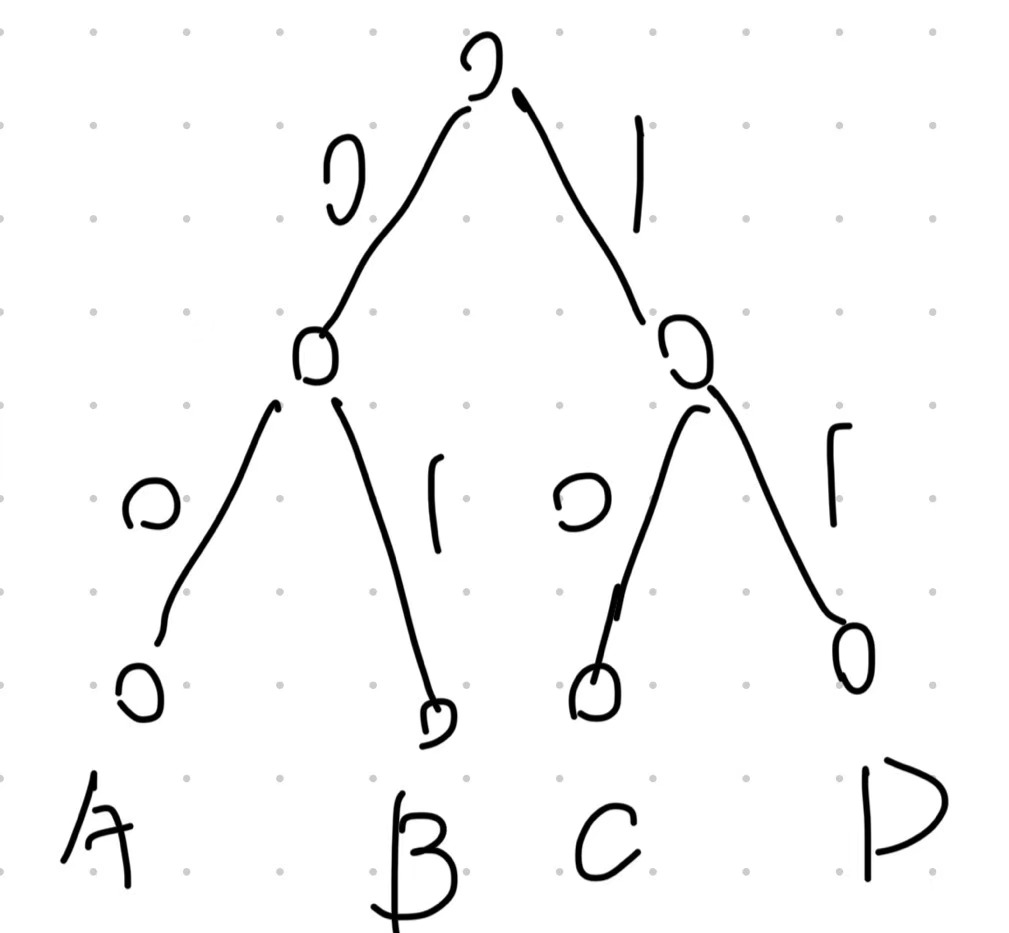
Then the problem equals to find a tree miminizes $\sum_{a\in S}f(a)|depth(a)|$.
For greedy strategy,we always select two node with the smallest frequency and attach them to a node to get a new node with the sum of their frequency.
It can easily prove that the solution is optimal.
Lemma
- Let $a$ and $b$ be two strings in $S$ with same frequency ,there is a optimal solution in which $a$ and $b$ are siblings.
- A binary tree that is not full cannot correspond to an optimal prefix code.
