Binomial Tree & Binomial Heap

⭐文章目录⭐

• Binomial Tree
  • Definition
  • Theorem
• Binomial Queue(Heap)
  • Definition
  • Lemma

👇

Binomial Tree

Here is an example of a binomial tree:

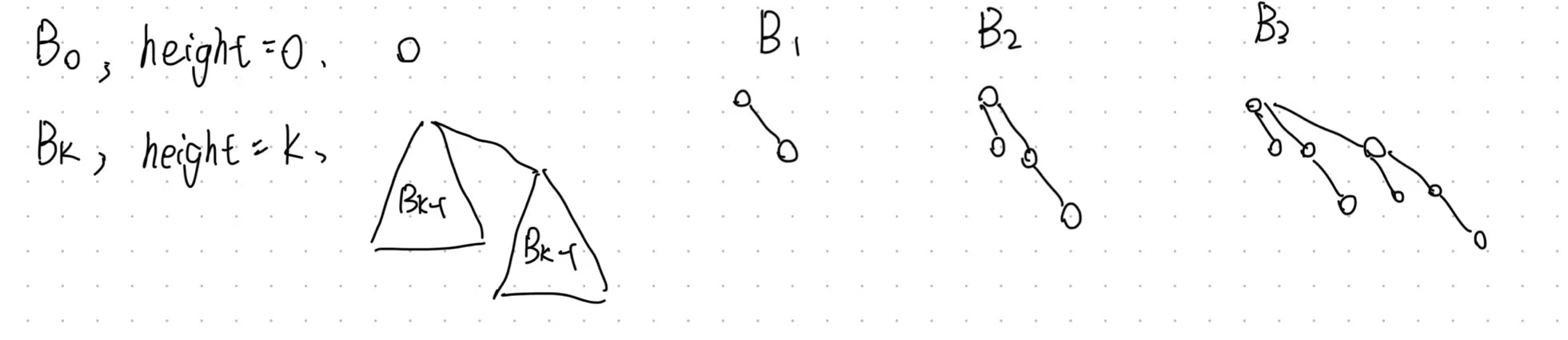
Definition

• A binomial tree $B_k$ is a tree with a height of k,which is generated by attaching $B_{k-1}$ to another $B_{k-1}$.

Theorem

• The number of children of the root of $B_k$ is $k$.
• The number of nodes in $B_k$ is $2^k$.
• The number of nodes at depth d at $B_k$ is $C_k^d$.

Binomial Queue(Heap)

Definition

• A binomial heap is a collection of binomial trees.
• Binomial trees in a binomial heap have different heights.
• Each of Binomial Trees satisfies the heap property.

Here is an example of a binomial heap:

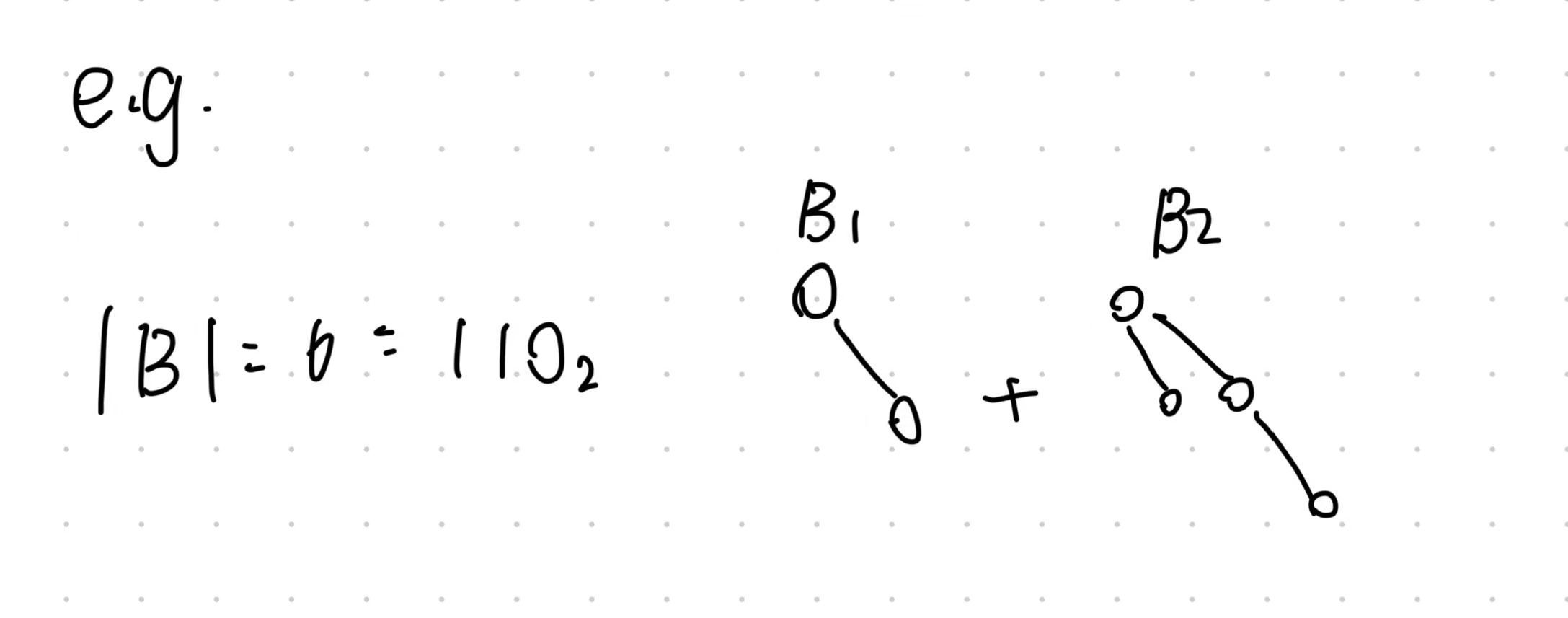
Lemma

• Number of Trees in a n-nodes binomial heap is under $log_2(n)$.
• $N$ insertions into an empty binomial heap takes $O(n)$ time.
• findmin(): $O(logn)$($O(1)$ with a pointer to the min root)
  • 1.1.find the $B_k$ with minimum root key.
  • 2.Return the minimum key.
• insert(): $O(logn)$
• merge($H_1, H_2$): $O(logn)$
  • 1.Let $k_1$ and $k_2$ be the max height of $H_1$ and $H_2$ respectively.
  • 2.For i in range(max($k_1, k_2$)):
  • 3.IF $B_i$ has two trees,combine them into one tree.
• deletemin(): $O(logn)$
  • 1.find the $B_k$ with minimum root key.
  • 2.H = H - $B_k$
  • 3.H’ = $B_K$ - root
  • 4.merge(H, H’)
• decreasekey($x, k$): $O(logn)$
  • Do as normal heap does.
• delete($x$): $O(logn)$
  • 1.decreasekey($x, \infty$)
  • 2.deletemin()

BinQueue  Merge( BinQueue H1, BinQueue H2 )
{	BinTree T1, T2, Carry = NULL; 	
	int i, j;
	if ( H1->CurrentSize + H2-> CurrentSize > Capacity )  ErrorMessage();
	H1->CurrentSize += H2-> CurrentSize;
	for ( i=0, j=1; j<= H1->CurrentSize; i++, j*=2 ) {
	    T1 = H1->TheTrees[i]; T2 = H2->TheTrees[i]; /*current trees */
	    switch( 4*!!Carry + 2*!!T2 + !!T1 ) { 
		case 0: /* 000 */
	 	case 1: /* 001 */  break;	
		case 2: /* 010 */  H1->TheTrees[i] = T2; H2->TheTrees[i] = NULL; break;
		case 4: /* 100 */  H1->TheTrees[i] = Carry; Carry = NULL; break;
		case 3: /* 011 */  Carry = CombineTrees( T1, T2 );
			            H1->TheTrees[i] = H2->TheTrees[i] = NULL; break;
		case 5: /* 101 */  Carry = CombineTrees( T1, Carry );
			            H1->TheTrees[i] = NULL; break;
		case 6: /* 110 */  Carry = CombineTrees( T2, Carry );
			            H2->TheTrees[i] = NULL; break;
		case 7: /* 111 */  H1->TheTrees[i] = Carry; 
			            Carry = CombineTrees( T1, T2 ); 
			            H2->TheTrees[i] = NULL; break;
	    } /* end switch */
	} /* end for-loop */
	return H1;
}

ElementType  DeleteMin( BinQueue H )
{	BinQueue DeletedQueue; 
	Position DeletedTree, OldRoot;
	ElementType MinItem = Infinity;  /* the minimum item to be returned */	
	int i, j, MinTree; /* MinTree is the index of the tree with the minimum item */

	if ( IsEmpty( H ) )  {  PrintErrorMessage();  return –Infinity; }

	for ( i = 0; i < MaxTrees; i++) {  /* Step 1: find the minimum item */
	    if( H->TheTrees[i] && H->TheTrees[i]->Element < MinItem ) { 
		MinItem = H->TheTrees[i]->Element;  MinTree = i;    } /* end if */
	} /* end for-i-loop */
	DeletedTree = H->TheTrees[ MinTree ];  
	H->TheTrees[ MinTree ] = NULL;   /* Step 2: remove the MinTree from H => H’ */ 
	OldRoot = DeletedTree;   /* Step 3.1: remove the root */ 
	DeletedTree = DeletedTree->LeftChild;   free(OldRoot);
	DeletedQueue = Initialize();   /* Step 3.2: create H” */ 
	DeletedQueue->CurrentSize = ( 1<<MinTree ) – 1;  /* 2MinTree – 1 */
	for ( j = MinTree – 1; j >= 0; j – – ) {  
	    DeletedQueue->TheTrees[j] = DeletedTree;
	    DeletedTree = DeletedTree->NextSibling;
	    DeletedQueue->TheTrees[j]->NextSibling = NULL;
	} /* end for-j-loop */
	H->CurrentSize  – = DeletedQueue->CurrentSize + 1;
	H = Merge( H, DeletedQueue ); /* Step 4: merge H’ and H” */ 
	return MinItem;
}