⭐文章目录⭐
👇
B+ Tree
The following picture is a a example of a B+ Tree of order 3.
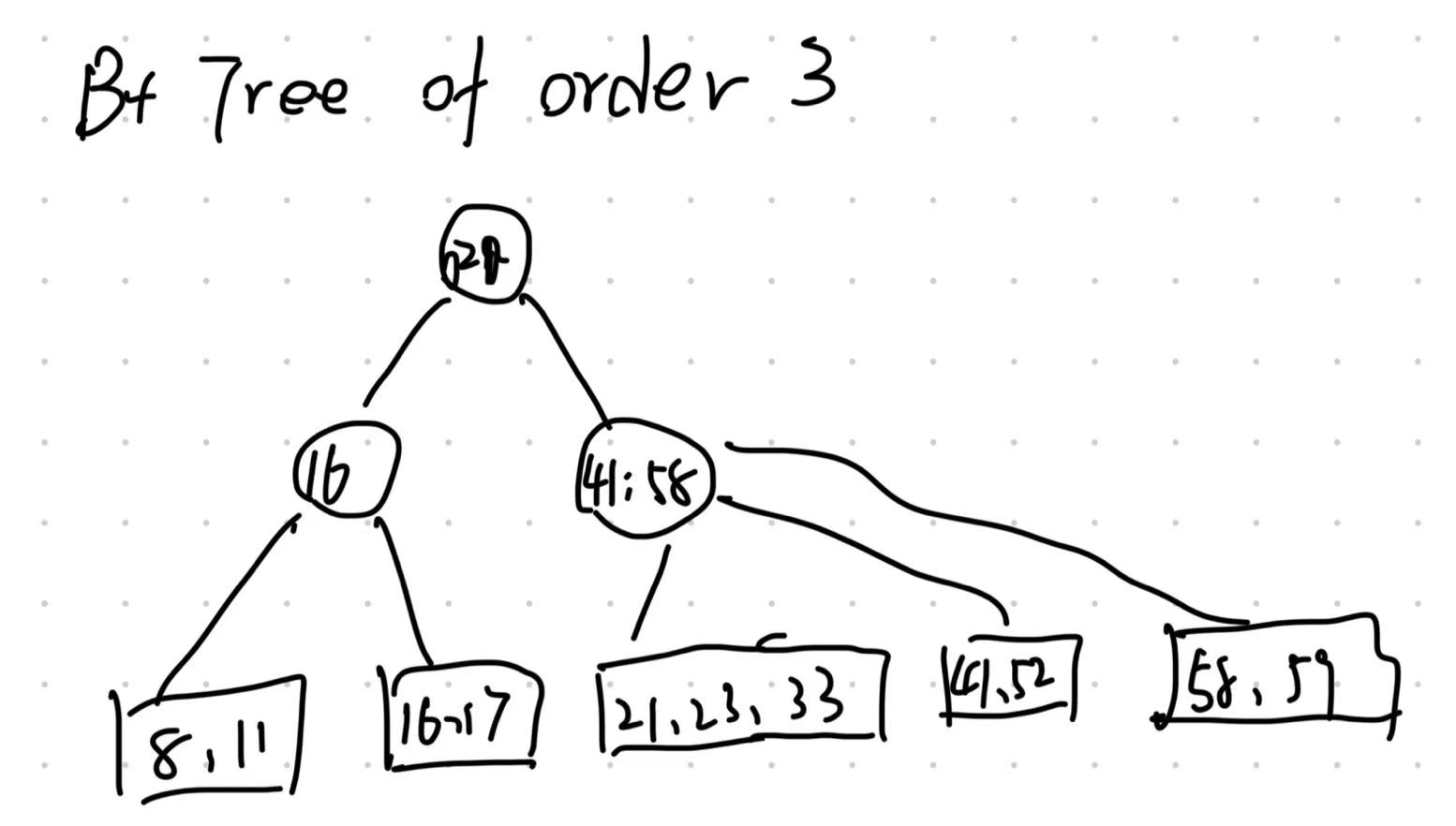
Definition
- B+ Tree of Order B
- 1.all leaves are at the same level
- 2.data elements are stored in the leaves.
- 3.$\lceil \frac{B}{2}\rceil \leq$ fan-out of any internal node $\leq B$
- 4.$\lceil \frac{B}{2}\rceil \leq$ number of elements in a leaf $\leq B$
- 5 .in a internal node,the $i$-th number $e_i = $ the minimum element stored in leaves of its $(i+1)$-th children.
- 6.$N$,number of elements in the tree, should be larger than $B$.
Theorem
- number of leaves $\leq \frac{N}{\lceil \frac{B}{2}\rceil}$.
- number of nodes $\leq \frac{2N}{\lceil \frac{B}{2}\rceil}$.
- cost of space = $\leq \frac{2N}{\lceil \frac{B}{2}\rceil}\times B\leq 4B$.
- height $\leq log_{\lceil \frac{B}{2}\rceil}(\frac{N}{\lceil \frac{B}{2}\rceil})\leq log_{\lceil \frac{B}{2}\rceil}(N)\leq \frac{logN}{log(B-1)}=O(log_BN)$.
- findkey(): $O(log_BN)$
- insert(): $O(log_BN)$
- delete(): $O(log_BN)$
Insertion
- 1.Search for the leaf node where the new element should be inserted.
- 2.Insert the new element into the leaf node.
- 3.If the number of elements in the leaf node exceeds $B$, split the leaf node into two new leaf nodes.
- 4.If the number of elements in the parent node exceeds $B$, split the parent node into two new parent nodes.
- 5.Repeat step 4 until the property of B+ Tree is satisfied.
Deletion
- 1.Search for the leaf node containing the element to be deleted.
- 2.Delete the element from the leaf node.
- 3.If the number of elements in the leaf node is less than $\lceil \frac{B}{2}\rceil$:
- if the sibling has at least $\lceil \frac{B}{2}\rceil+1$ elements, take one from the sibling.
- if the sibling has less than $\lceil \frac{B}{2}\rceil+1$ elements, merge the sibling.
- 4.Update the parent nodes to maintain the B+ Tree property.
Heaps
Leftist Heap
- it contains heap property.
- binary tree satisfying leftist property.
- let $npl(u)$ equals to the length of the shortest path from $u$ to a leaf.
- leftist property: right path from root to leaf is the shortest path from root to any leaf
$\leftrightarrow$ $npl(u$->$right)\leq npl(v$->$left)$.
Theorem
- A leftist tree with $r$ nodes on the right path must have at least $2^r – $1 nodes.
- For a leftist heap with n nodes, its right path from root to null has at most $log_2(n)$ nodes.
Merge Operation
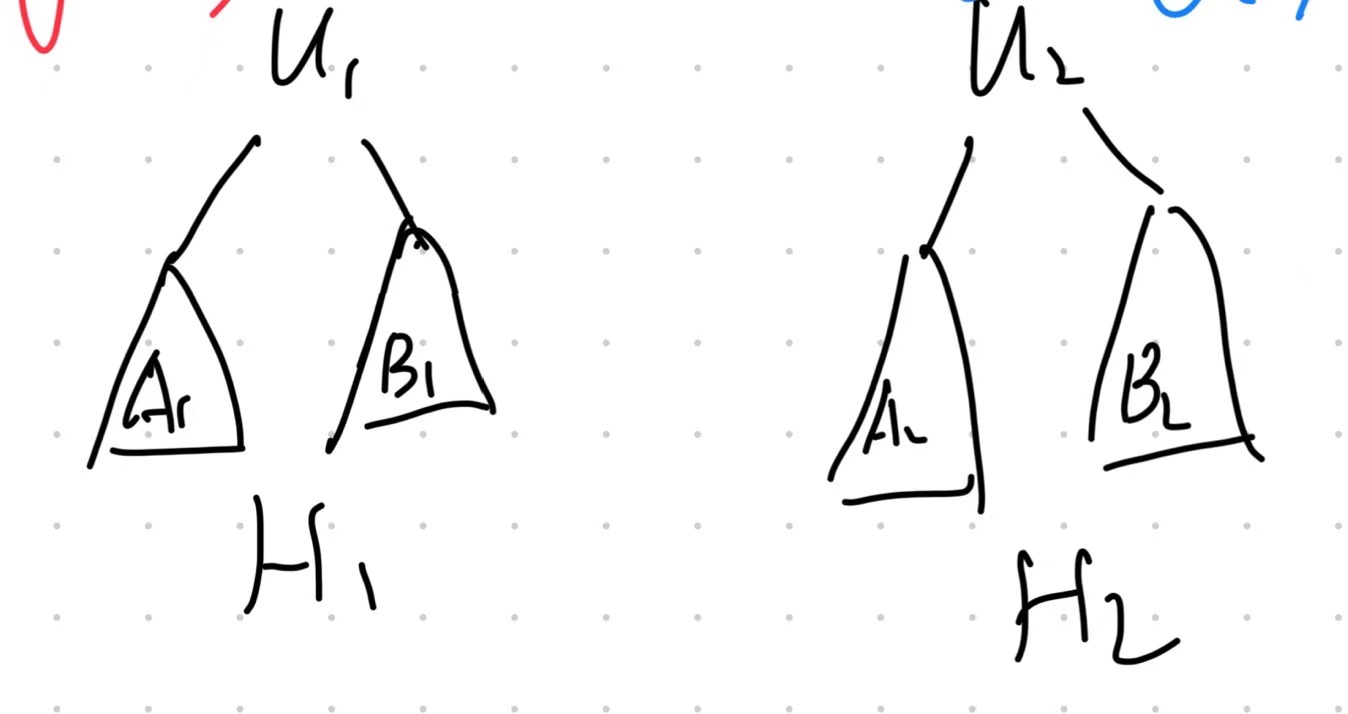
merge(H1, H2):
case 1: H1 is empty
return H2
case 2: H2 is empty
return H1
case 3: (assume u1 < u2)
B'=merge(B1,H2)
if npl(A1->root) >= npl(B'->root):
H = the right form in the picture below
else :
H = the right form in the picture below
update npl(u1)
return H
(number of recursions is |H1|+|H2|)
- This operation takes $O(logn)$ time in amortized and worst case.
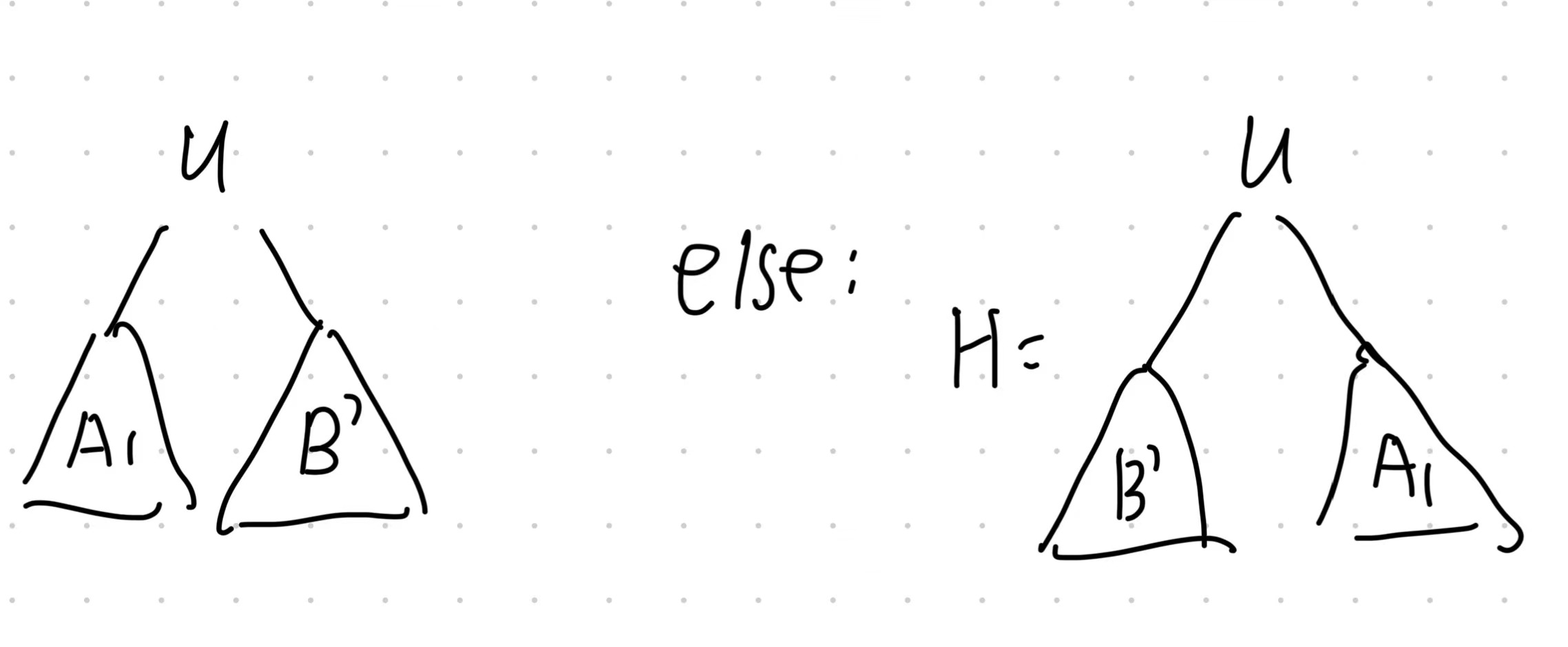
Insertion Operation
- merge()
Delete-min Operation
- delete root
- merge the subtrees of the root
Delete-key Operation
- find the node containing the key
- delete the node
- merge the subtrees of the node
- attach the merged subtree to the parent node
- this may lead to not leftist property, so we need to fix it.
Fixing the Property
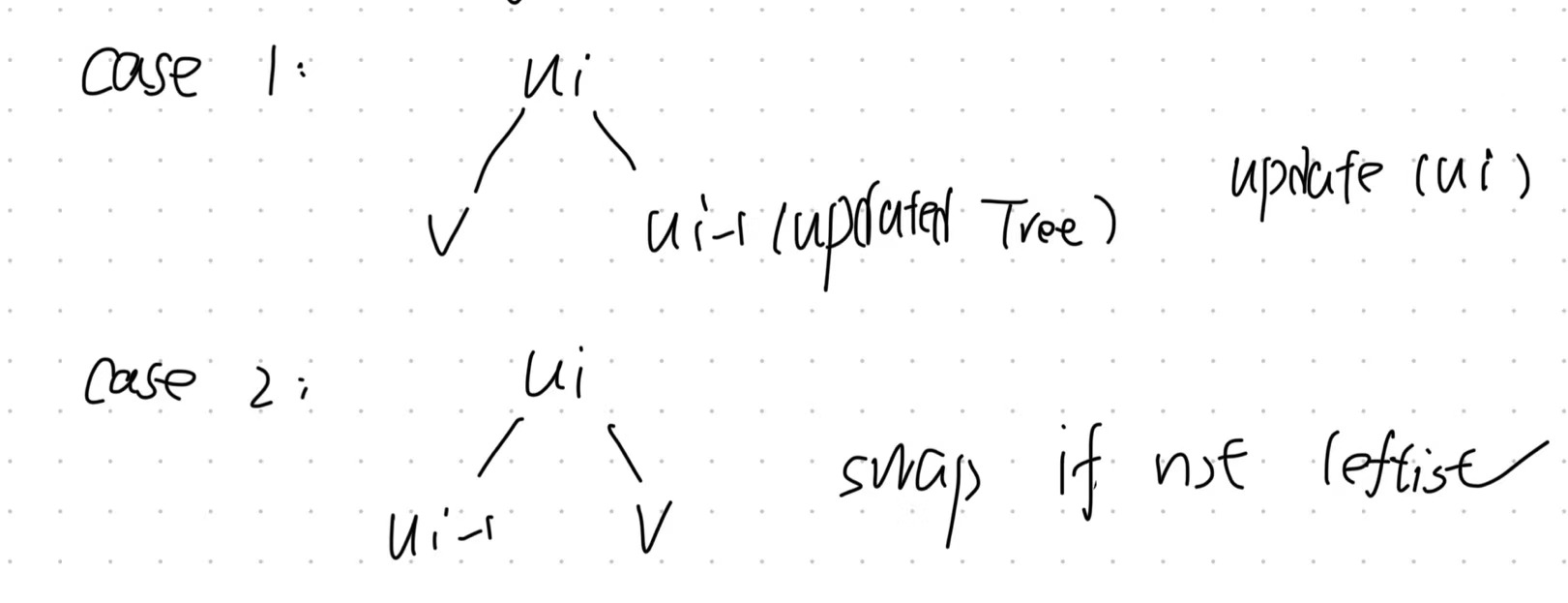
- Find the first node that violates the leftist property from the parent node of the deleted node to the root.
- Swap its children and step above.
- Repeat until the property is satisfied.
- Update the npl of the nodes.
Skew Heap
Merge Operation
merge(H1, H2):
case 1: H1 is empty
return H2
case 2: H2 is empty
return H1
case 3: (assume u1 < u2)
B'=merge(B1,H2)
H = the right form in the picture below(always swap)
update npl(u1)
return H
(number of recursions is |H1|+|H2|)
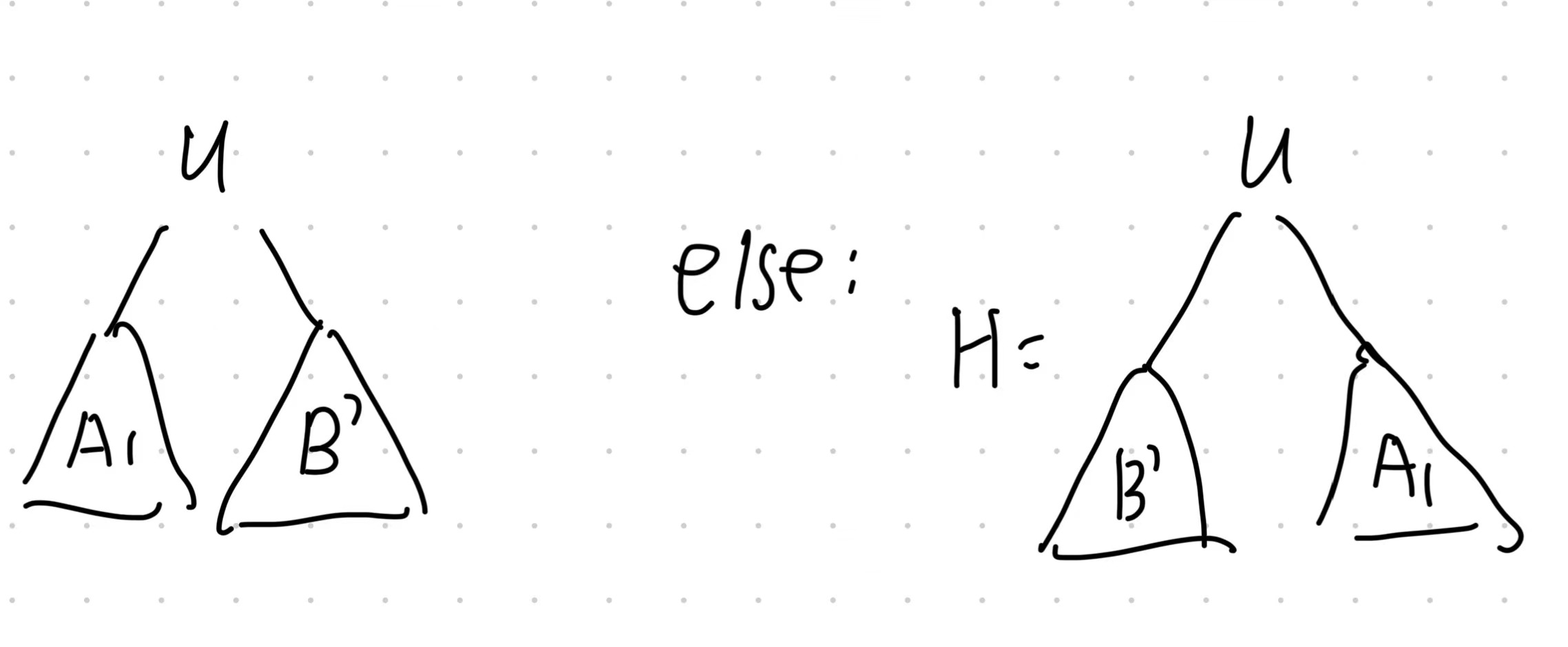
- Heavy node is the node in the skew heap whose number of children in the right subtree is greater than the number of children in the left subtree.
- After merging,all the heavy node on the right path will turn into a light node,but not all light nodes on thr right path will turn into heavy nodes.
- For the nodes not on the right path, their properties remain unchanged.
Theorem
- Any $M$ consecutive operations take at most $O(M log N)$ time.
Comparison
| min-heap | leftist-heap | skew-heap | |
|---|---|---|---|
| build() | $O(n)$ | $O(n)$ | $O(n)$ |
| merge() | $O(n)$ | $O(logn)$ | worst $O(n)$,amortized $O(logn)$ |
