⭐文章目录⭐
👇
Amortized Analysis
Definition
- Any $M$ consecutive operations take at most $O(M log N)$ time.
- Amortized time bound.
- $T_{worst}\geq T_{amortized}\geq T_{average}\geq T_{best}$
Aggregate analysis
Definition
- Show that for all $n$, a sequence of $n$ operations takes worst-case time $T(n)$ in total. In the worst case, the average cost, or amortized cost, per operation is therefore $T(n)/n$.
Example: Dynamic Array
Definition
- A dynamic array is a array with initial capacity $1$.
- When the array is full,it doubles its capacity.
Insertion
-
It takes $O(n)$ in worst case but amortized time is $O(1)$ per operation.
-
We define $W(m)$ as the cost of a sequence of $m$ insertions into an initially empty dynamic array.
-
$T(m)=mc + (1 +2)c+ (2+4)c+…+(2^k+2^{k+1})c$,where $k= log_2(n)$.
-
In the given formula, $c$ is a constant, $mc$ refers to the cost of write $m$ elements into the array, and in the $(2^k+2^{k+1})c$ term,$2^kc$ refers to the cost of copying the array while $2^{k+1}c$ refers to the cost of creating a new array with doubled capacity.
-
$T(m)=mc + (1 +2)c+ (2+4)c+…+(2^k+2^{k+1})c\leq mc+6mc=7mc$
-
$T_{amortized}=\frac{T(m)}{m}=7c=O(1)$
Accounting Method
Definition
- When an operation’s amortized cost exceeds its actual cost, we assign the difference to specific objects in the data structure as credit. Credit can help pay for later operations whose amortized cost is less than their actual cost.
- $T_{amortized} = T_{actual} + T_{credit}$
Example: Two-Stack Queue
- A Two-Stack Queue is a queue with two stacks,one for input and one for output.
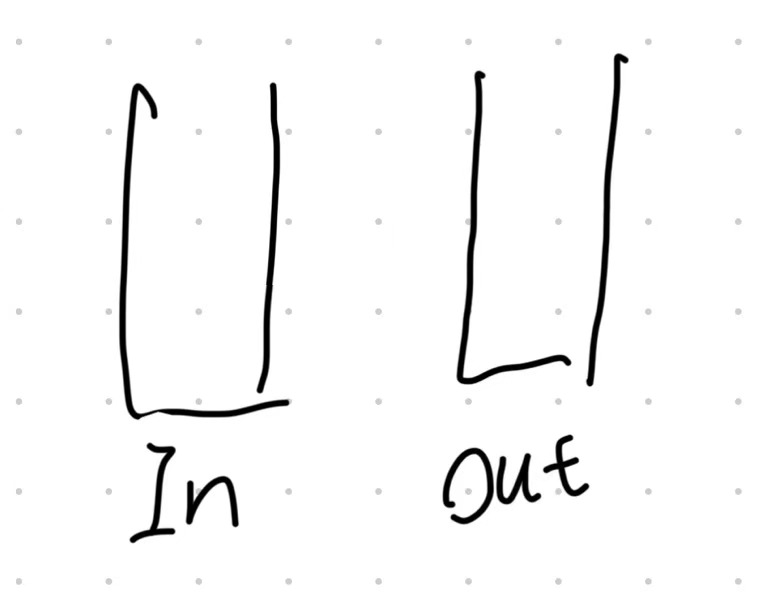
Enqueue Operation
In.push(x)
Dequeue Operation
if out.not_empty():
out.pop()
else if In.not_empty():
while In.not_empty():
x = In.pop()
out.push(x)
out.pop()
- Enqueue operation takes $O(1)$ time in the worst case.
- Dequeue operation takes $O(n)$ time in the worst case.
- Amortized time for enqueue and dequeue operation is $O(1)$ per operation.
Amortized Analysis
| acutal | credit | amortized | |
|---|---|---|---|
| Enqueue | $c$ | $2c$ | $3c$ |
| Dequeue | $2c\times$|$In$|$+c$ | $-2c\times$|$In$| | $c$ |
- It can be easily seen that the amortized time for enqueue and dequeue operation is $O(1)$ per operation.
- And the credit accumulated will always larger than 0.
Potential Function
Definition
- $\phi(i)$ equals to the total number fo credits remaing after $i$ operations.
- $\phi(i)$ is a potential function.
- $\Delta\phi(i) = \phi(i)-\phi(i-1)$.
- $T_{amortized}(i) = T_{actual}(i) + \Delta\phi(i)$
- $\phi(i) \geq \phi(0)$
Example: Two-Stack Queue
- $\phi(0) = 0$
- $\phi(i)$ equals to the number of elements in the input stack after $i$ operations.
Splay Tree
Definition
- $splay(u)$ is rotate $u$ to the root of the tree.
- $findkey()$
- 1.find as BST
- 2.splay the node to root
- $insert()$
- 1.insert as BST
- 2.splay the node to root
- $delete()$
- 1.splay the node to root
- 2.delete it.
- 3.if u has only one child,finish.
- 4.if u has two children,splay the largest node in the left subtree(or the smallest node in the right subtree) and attach another subtree to it.
Splay Operation
case 1: u is a child of the root
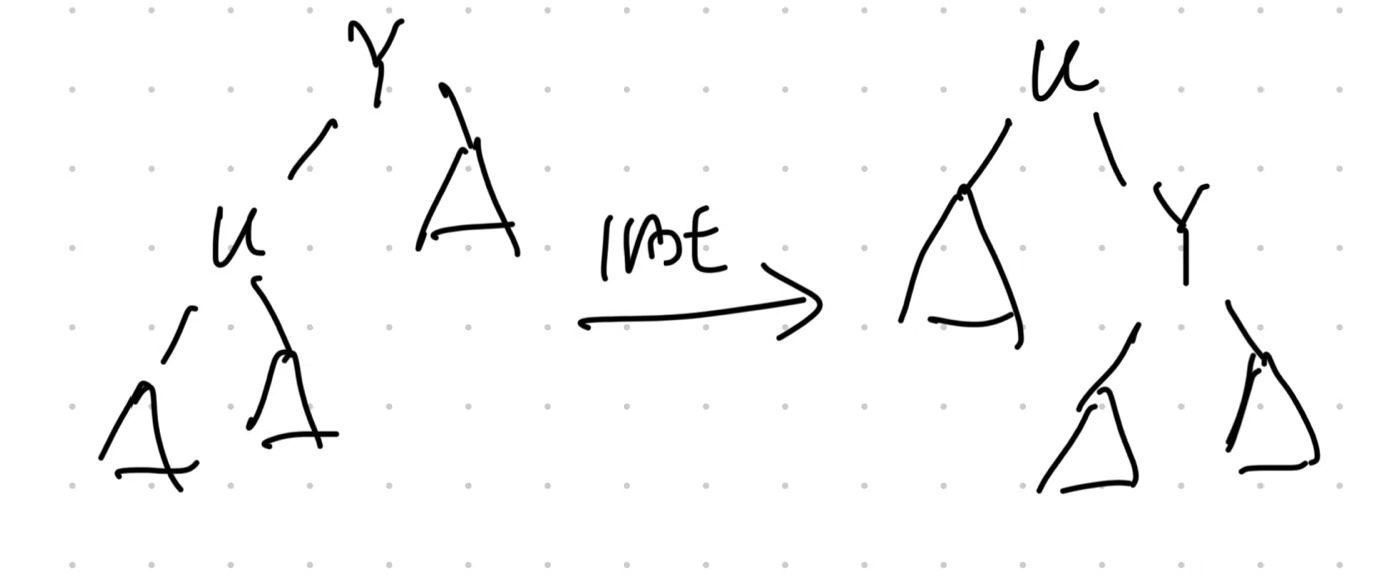
- Perform a Rotation on $u$.
case 2: u has grandparent
case 2-1:zig-zag
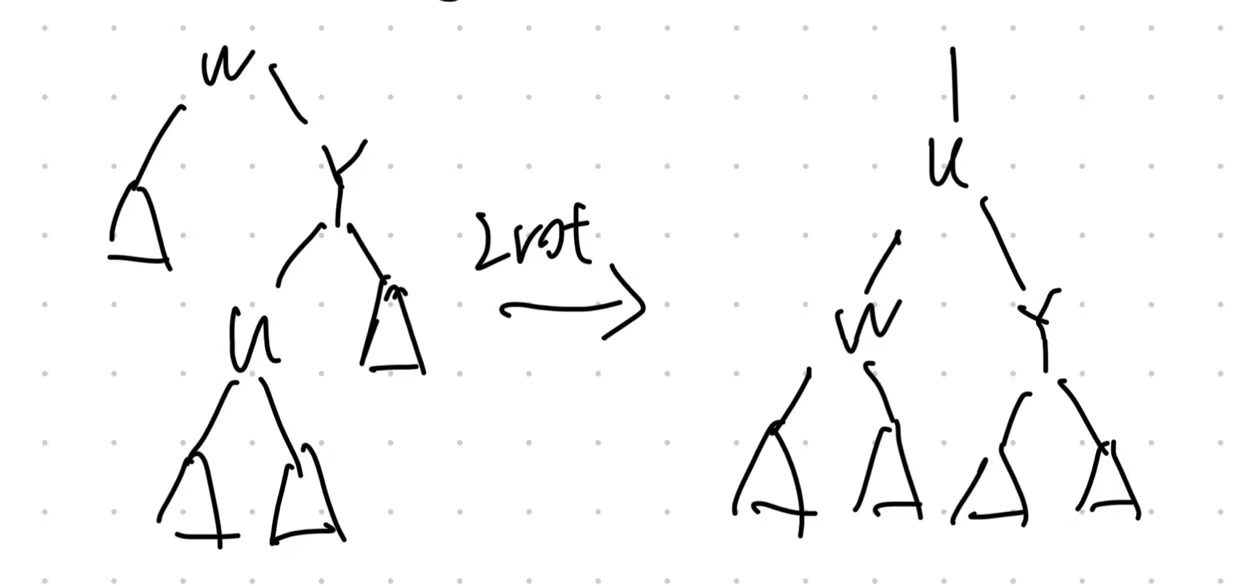
- Perform a Rotation on $u$ to make it as the parent of its orignial parent $Y$.
- Perform a Rotation on $u$ to make it as the parent of its parent original $Y$ and original grandparent $w$.
case 2-2:zig-zig
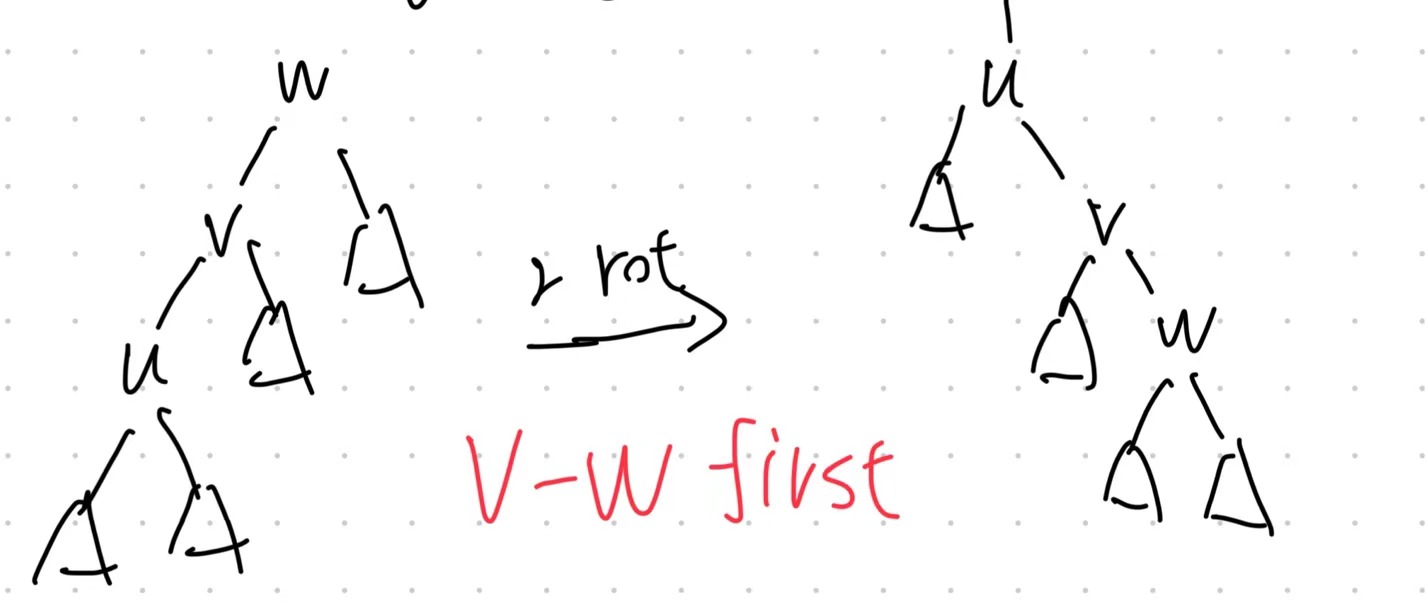
- Perform a Rotation on $v$ to make it as the parent of its orignial parent $w$.
- Perform a Rotation on $u$ to make it as the parent of its parent original $v$.
Time Complexity Analysis
- Given a BST $T_{u}$
- For each $u \isin T$, $T_{u}$ is the subtree rooted at $u$.
- $\delta(u)=log(|T_{u}|)$
- $\phi(T)=c\sum_{u \in T} \delta(u)$
- $T’$ is the splay tree after $splay(u)$ on T.
- $\Delta\phi(T’)=\phi(T’)-\phi(T)\leq 3c(\delta’(u)-\delta(u))-2c\times|Rotations-1|$
The amortized time to splay a tree with root T at node X is at most
3( R( T ) – R ( X ) ) + 1 = O(log N).
