⭐文章目录⭐
👇
Incomputable Problems
Halting Problem
Definition
Given a problem $p$ and an input $x$, the halting problem asks whether $p$ halts on input $x$.
Proof
- Assume that there exists a program $HALT$ that have the following properties:
- $HALT(p,x) = 1$ if $p$ halts on input $x$
- $HALT(p,x) = 0$ otherwise.
- Then we can define a new function :
Diagonal(p):
if Halt(p,p)==1:
while(true);
else:
terminate;
We have:
- $Diagnoal(p)$ terminates if $p$ does not halt on input $p$.
- $Diagonal(p)$ loops forever if $p$ halts on input $p$.
Then ,let $p$ =Diagonal,we have: - $Diagnoal(p)$ terminates if Diagnoal does not halt on input Diagonal.
- $Diagonal(p)$ loops forever if Diagonal halts on input Diagonal.
It’s obvious that it is impossible.
Therefore,there is no algorithm that can solve the halting problem.
Postpone Corresponding Proble(PCP)
Not for details.
Turing Machines
- A Deterministic Turing Machine (DTM) executes one instruction at each point in time. Then depending on the instruction, it goes to the next unique instruction.
- A Nondeterministic Turing Machine(NDTM) is free to choose its next step from a finite set. And if one of these steps leads to a solution, it will always choose the correct one.
Complexity Classes
$P,NP,EXP,PSPACE…$
Lemma
$P\subseteq NP$
Examples
Given a weighted graph $G$, two vertice $s,t$
1.What is the shortest path from $s$ to $t$ in $G$?
2.Length of the shortest path?
3.give a integer $k$ ,$\exist s -> t$ with length $\leq k$ in $G$?
For problems like $(3)$, we can have two answers: $yes$ or $no$.
So we define the input instances that make the answer of problems to be $yes$ are called $Yes$ $Instance$.On the other hand, the input instances that make the answer of problems to be $no$ are called $No$ $Instance$.
Then We define $A$ solves a problem $x$ if for every instance $I$ of $x$ :$A(I)=yes$ if and only if $I$ is $Yes$ $Instance$.
$P$ class
Definition
$A$ has a polynomial running time if there has a polynomial function $p()$ so that for any Instance $I$, A terminates on I with $O(P(|I|))$ steps. In other words, $A$ is in $P$ if it can be solved in polynomial time.
$P$ is the set of all decision problems that admit polynomial-time algorithms.
$NP$ class
Definition
$NP$ is polynomial-time verifiable problems. In other words, problem $P$ is in $NP$ if it can be proved to be solved in polynomial time.
$$V(x,t)=\begin{cases}1\quad if \ t \ certify \ x \\0 \quad otherwise \end{cases}$$
$$V(I,t)=\begin{cases}1\quad if \ I \ satifices \ F \\0 \quad otherwise \end{cases}$$
We say a =$V$ is a efficient verifier for a problem $x$ if :
- $V$ is a polynomial-time algorithm that takes two arguments: instance $I$ adm $t$.
- For any Instance $I$ of $x$, $I$ is an yes-instance if and only if: there exists a proof $t$ with $|t|\leq poly(|I|)$ and $V(I,t)=1$ .
Examples
- 3-SAT Problems
- e.g. Given $F:(x_1\cap x_2\cap x_3)\cup (x_2\cap \bar{x_3}\cap \bar{x_5})\cup (x_1\cap x_4)$
- If there exists a set of ${x}$, F=1.
- Hamiltonian Cycle Problems(HCP)
- Given a graph $G=(V,E)$, a HCP asks whether there exists a cycle that visits a;; vertices exactly once in $G$.
Lemma
It’s not known whether $P=NP$ or not.
Polynomial-time Reducible
We have two problems $x,y$, there instances $I_x,I_y$ and a reduction function $f$ that maps $I_x$ to $I_y$.
- $I_x$ is $Yes$ $Instance$ if and only if $I_y=f(I_x)$ is $Yes$ $Instance$.
If $\exist$ polynomial-time algorithm $B$ for $y$:
- $A(I_x)$:
- 1.compute $I_y=f(I_x)$
- 2.run $B$ on $I_y$ and return the result.
$I_x \rightarrow I_y=F(I_x) \rightarrow B(I_y)$
Because each steps takes polynomial time, so the total running time of $A$ is polynomial.
Then we can say $A\leq_P B$ if there exists the reduction function $f$.
Example1
Travling Salesman Problem(TSP)
- Given a complete edge-weighted graph $G=(V,E)$, a TSP asks to find a Hamiltonian cycle with total weight $W\leq k$ in $G$.
Proof $HCP\leq _PTSP$
As the picture shows:
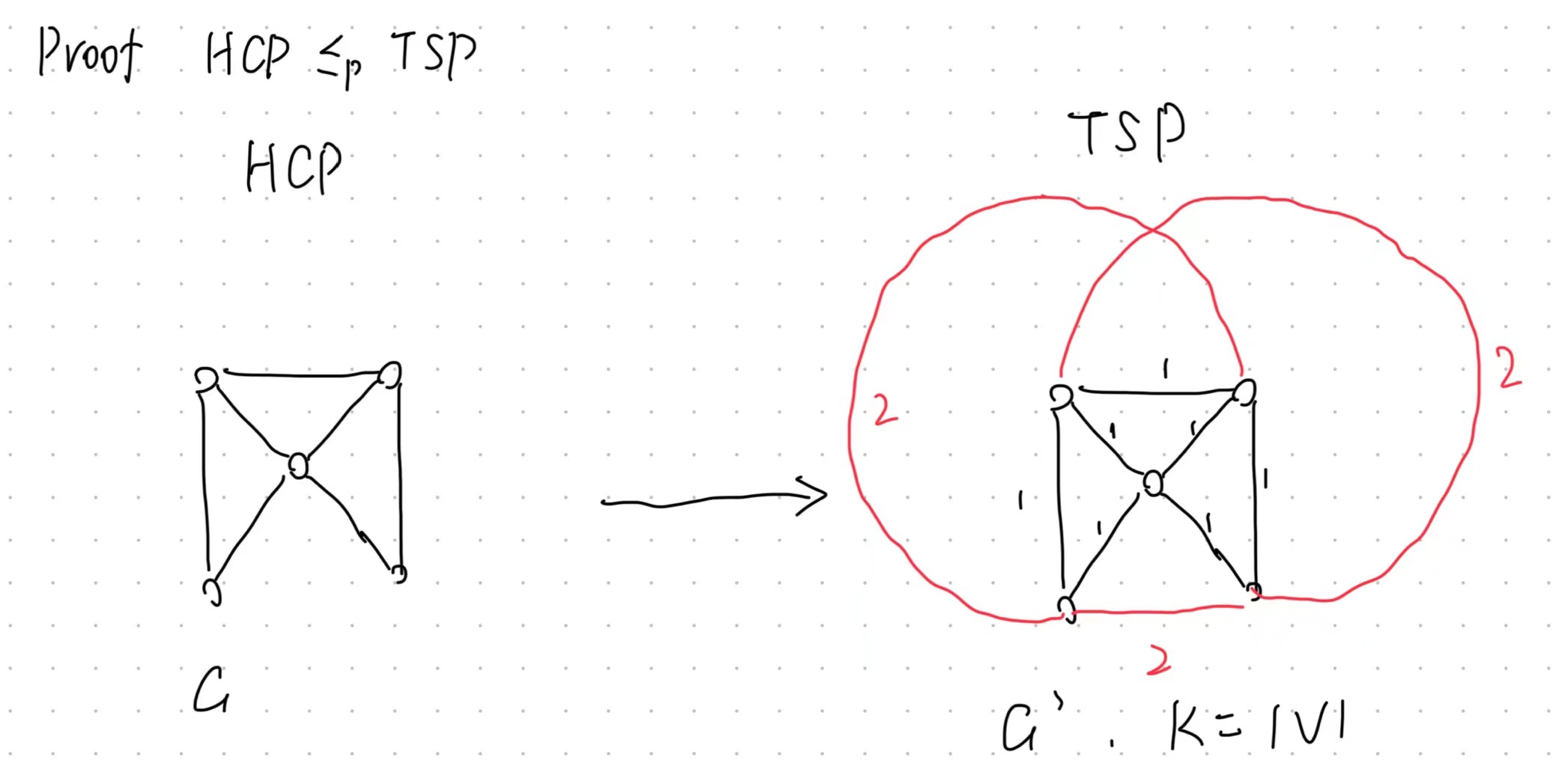
-
We can turn the $HCP$ Graph into a $TSP$ Graph by giving the weight of each edge as $1$ and adding the edges that connect the unconnected vertices with weight $2$.
- We can easily find the $yes-intacnce$ in $HCP$ is the $yes-instance$ in $TSP$.
-
So $HCP\leq _P TSP$.
Example2
- Clique Problem
- Given a graph $G=(V,E)$, a clique problem asks whether $G$ has a subset vetices $V’$ with size $|V’|\leq k$ such that $V’\times V’\subseteq E$.
- Vertex Cover Problem
- Given a graph $G=(V,E)$, a vertex cover problem asks whether $G$ has a subset of vertices $V’$ with size $|V’|\leq k$ such that every edge in $E$ is incident to at least one vertex in $V’$.
Proof $CP\leq _P VCP$
As the picture shows:
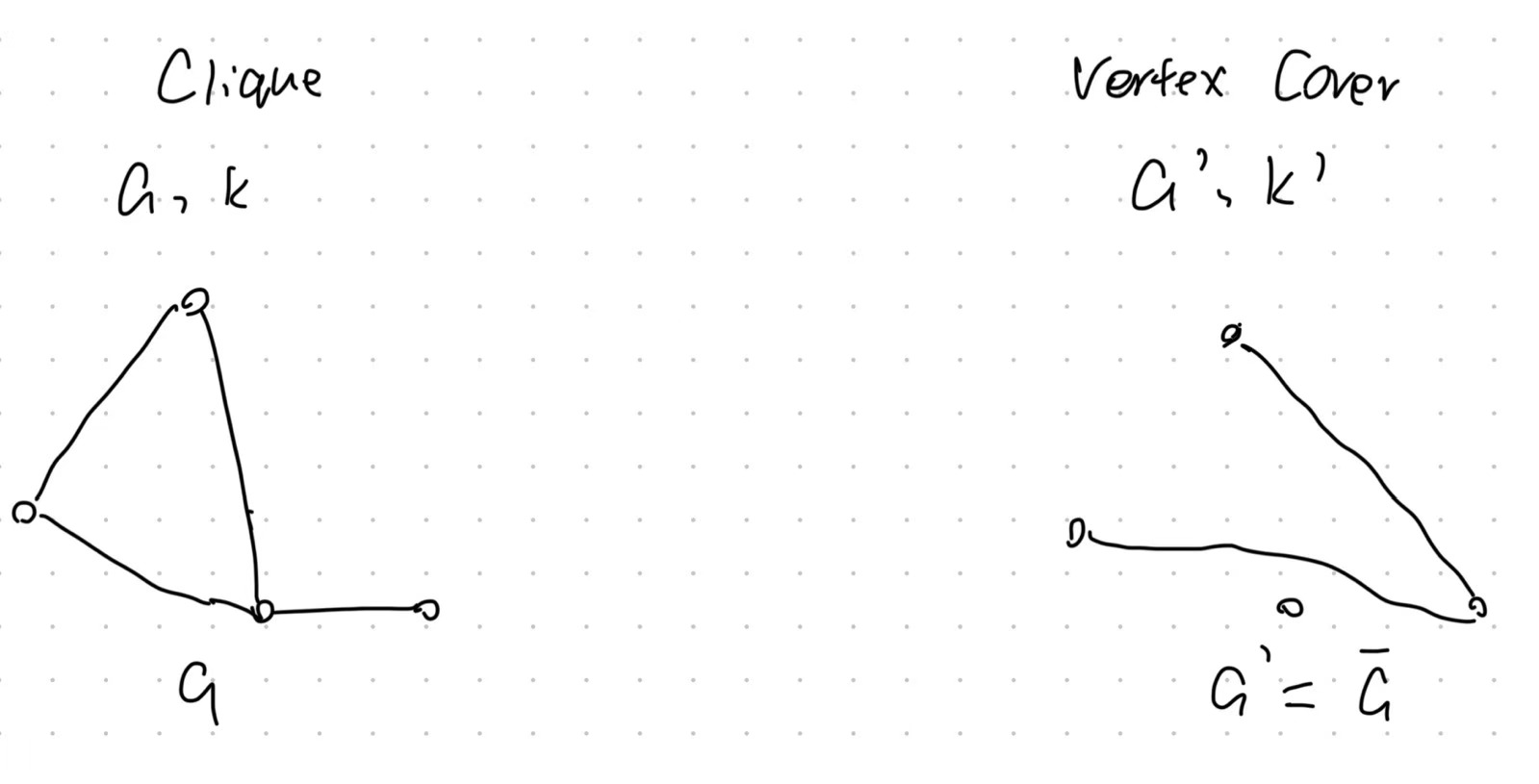
- We can turn the $CP$ Graph into a $VCP$ Graph by make $G_{VCP} = \bar {G_{CP}}$.
- If $V’$ is a clique in $G_{CP}$, then $V - V’$ is a vertex cover in $G_{VCP}$.
- If $V-V’$ is a vertex cover in $G_{VCP}$, then $V’$ is a clique in $G_{CP}$.
- And we can easily find the $yes-intacnce$ in $CP$ is the $yes-instance$ in $VCP$.
- So $CP\leq _P VCP$.
NP-Complete
Definition
A problem $x$ is NP-complete if it is in $NP$ and every problem in $NP$ is reducible to $x$.
Theorem
3-SAT, Vertex Cover, clique problems, Hamiltonian Cycle, Bin Packing and Domination Set problems are NP-complete.
Lemma
If NP-complete problem $x\isin P$, then $P=NP $.
NP-Hard
Definition
A problem $x$ is NP-hard if every problem in $NP$ is reducible to $x$.
Formula Language Framework
Abstract Problem
-
An abstract problem $Q$ is a binary relation on a set I of problem instances and a set $S$ of problem solutions.
-
An alphabet $\Sigma$ is a finite set of symbols
-
A language $L$ over $\Sigma$ is any set of strings made up of symbols from $Sigma$.
-
Denote empty string by $\epsilon$.
-
Denote empty language by $\emptyset$.
-
Language of all strings over $\Sigma$ is $\Sigma^*$.
-
The complement of $L$ is denoted by $\Sigma^*-L$.
-
The concatenation of two languages $L_1$ and $L_2$ is the language
$L = { x1x2 : x1 ∈ L1\ and\ x2 ∈ L2 }$. -
Algorithm $A$ accept a string $x$ if $A(x)=1$.
-
Algorithm $A$ reject a string $x$ if $A(x)=0$.
-
A language $L$ is decided by an algorithm $A$ if every binary string in $L$ is accepted by $A$ and every binary string not in $L$ is rejected by $A$.
-
To accept a language, an algorithm need only worry about strings in $L$, but to decide a language, it must correctly accept or reject every string in ${0, 1}^*$
-
$P = \lbrace L ⊆ {0, 1}^* : there\ exists\ an\ algorithm\ A\ that\ decides\ L\ in\ polynomial\ time\rbrace$.
-
A verification algorithm is a two-argument algorithm $A$, where one argument is an ordinary input string $x$ and the other is a binary string $y$ called a certificate.
-
A two-argument algorithm $A$ verifies an input string $x$ if there exists a certificate $y$ such that $A(x, y) = 1$.
-
The language verified by a verification algorithm $A$ is $L = \lbrace x ∈ {0, 1}^* : there\ exists\ y ∈ {0, 1}^* such\ that\ A(x, y) = 1\rbrace$.
-
A language $L$ belongs to $NP$ iff there exist a two-input polynomial-time algorithm $A$ and a constant $c$ such that $L = \lbrace x ∈ {0, 1}^* : there\ exists\ a\ certificate\ y\ with\ |y| = O(|x|c) such\ that\ A(x, y) = 1 \rbrace$. We say that algorithm $A$ verifies language $L$ in polynomial time.
co-NP Class
Definition
$co-NP$ class is the set of languages $L$ such that $\overline{L}\isin NP$.
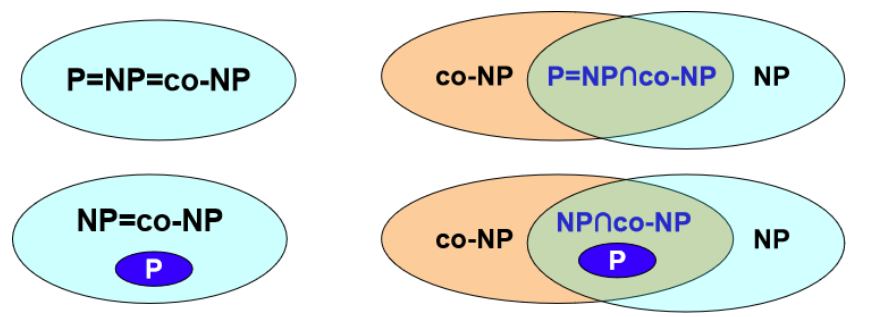
There are 4 possible relationships between $NP$,$P$ and $co-NP$ class: