⭐文章目录⭐
👇
AVL Tree(Balanced BST)
Weak Constraint
- $|H_{L}-H_{R}| \leq 1$ ($H_{L}-H_{R}$ is the balance factor of the Tree)
Rotation Operations
e.g. Right Rotation
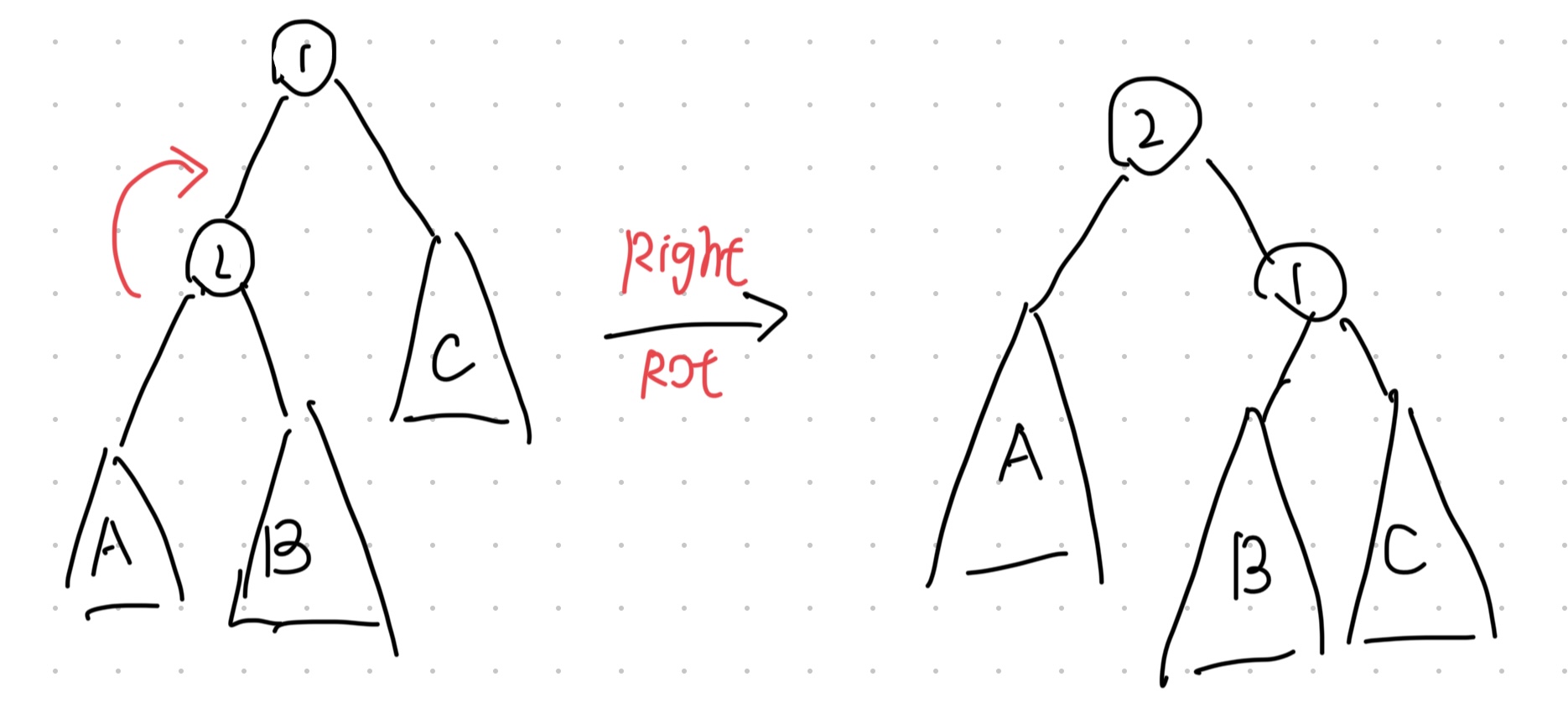
Left Rotation is the same as Right Rotation with the left and right subtrees swapped.
Insertion Operation
- 1.Insert as BST , which takes $O(n)$ time.
- 2.Restore the balance property of the AVL Tree,which takes $O(1)$ time.
Restore Operation
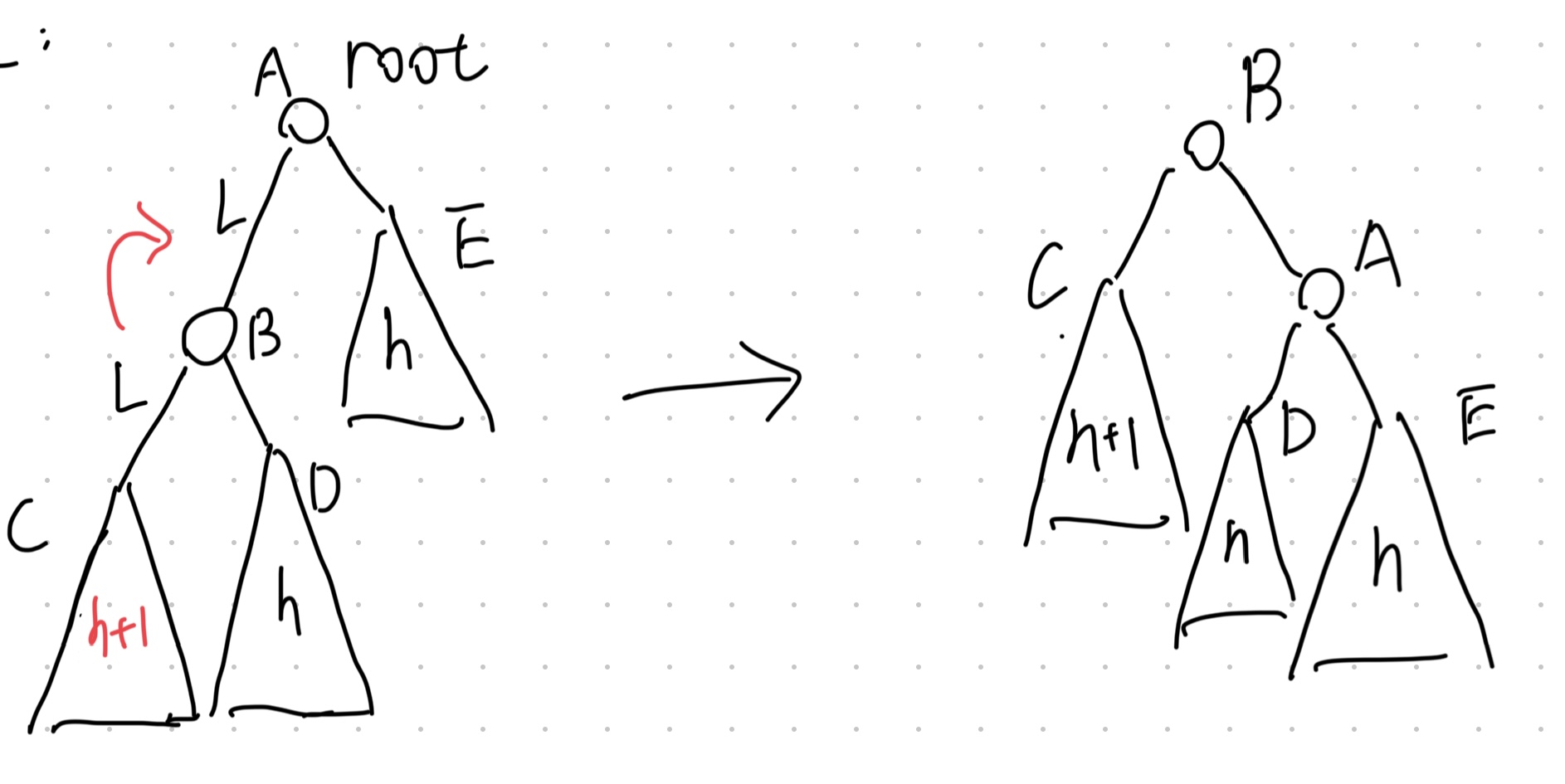
case 1: Left Left Case
It takes a Right Rotation to restore the balance property.
case 2: Right Right Case
It is the same as the Left Left Case with the left and right subtrees swapped.
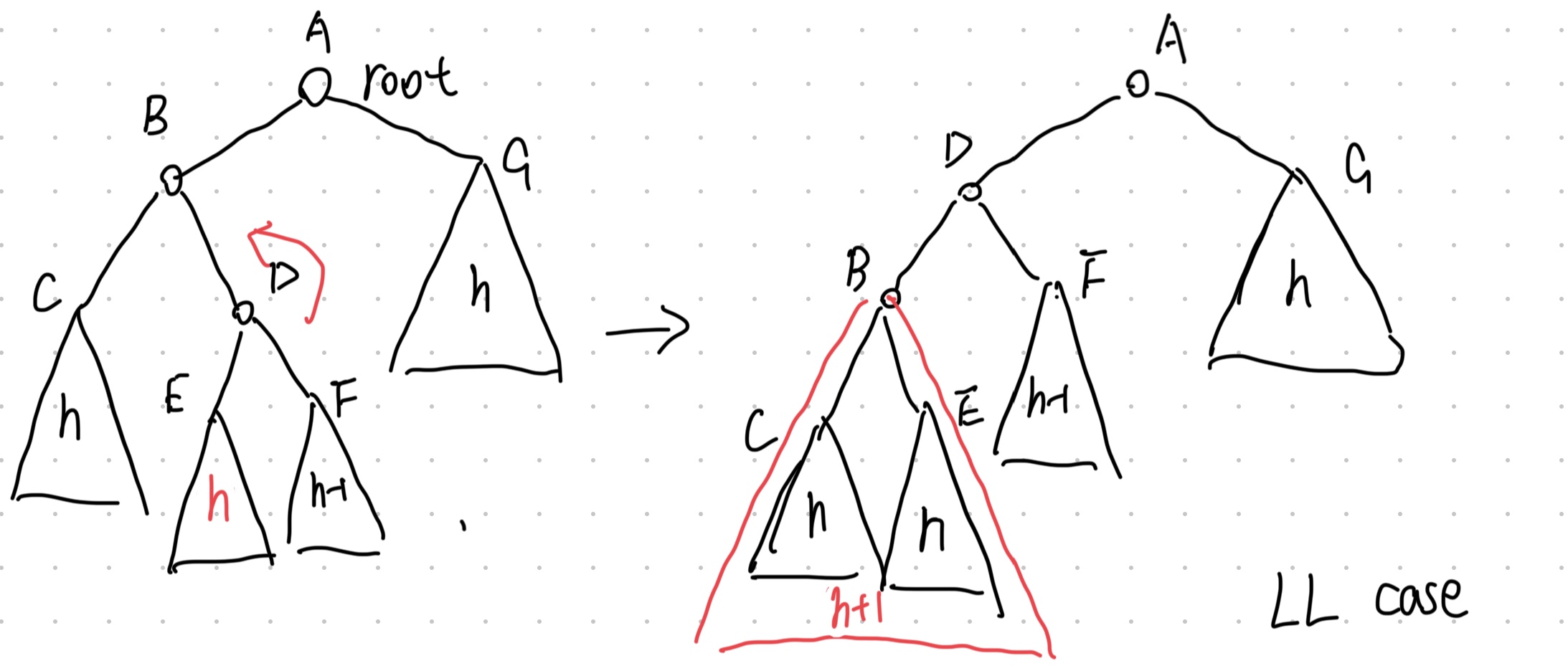
case 3: Left Right Case
It takes a Left Rotation to turn the case into the Left Left Case.Then just follow the left left case to restore the balance property.
case 4: Right Left Case
It is the same as the Left Right Case with the left and right subtrees swapped.
Deletion Operation
- 1.Delete as BST, which takes $O(log n)$ time.
- 2.Restore the balance property of the AVL Tree, which takes $O(log n)$ time.
Red-Black Tree(RBT)
Properties
- Every node is either red or black.
- The root is black.
- Every leaf (NULL) is black.
- The child of a red node is black.
- For each node $u$,all the paths from $u$ to its descendant leaves have the same Black-Height($bh(u)$),which equals to the number of black nodes on the path from $u$ to a leaf.
Theorem
- A red-black tree with $N$ internal nodes has height at most $2ln(N +1)$.
- $bh(Tree) > h(Tree) / 2$
Insertion Operations
- 1.Insert a red node as BST, which takes $O(log n)$ time.
- 2.Restore the balance property of the RBT, which takes $O(log n)$ time.
Restore After Insertion
case 1: The parent of the inserted node is black
Do nothing.

This case takes $O(1)$ time.
case 2: The parent of the inserted node is red
case 2-1: The sibling of the parent $u$ is red

- 1.Color the parent $u$ and sibling $v$ black.
- 2.Color the granBParent $p$ red if it is not the root.
- 3.Continue the case 2-1 process if parent of p is red.
This case takes $O(logn)$ time.
case 2-2: The sibling of the parent $u$ is black
case 2-2-1: The inserted node $I$ is the left child of the parent $u$
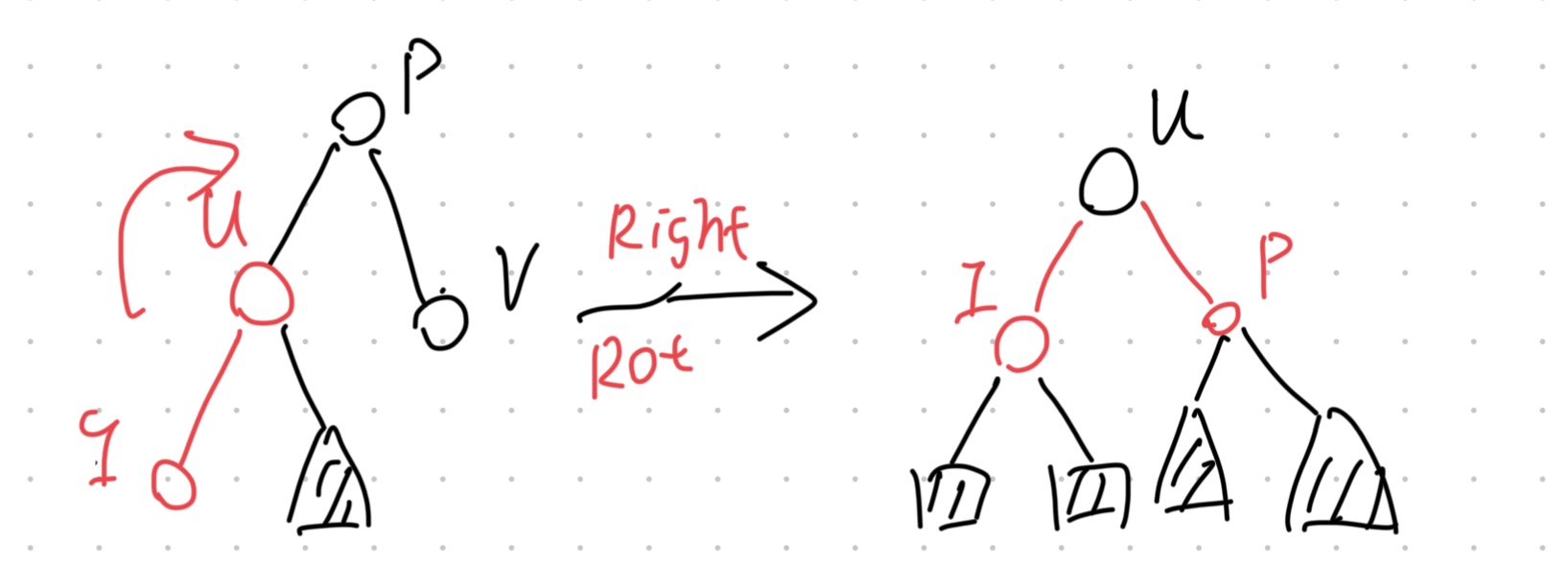
- 1.Perform a Right Rotation on the parent $u$.
- 2.Color $u$ black and $p$ red.
This case takes $O(1)$ time.
case 2-2-2: The inserted node $I$ is the right child of the parent $u$
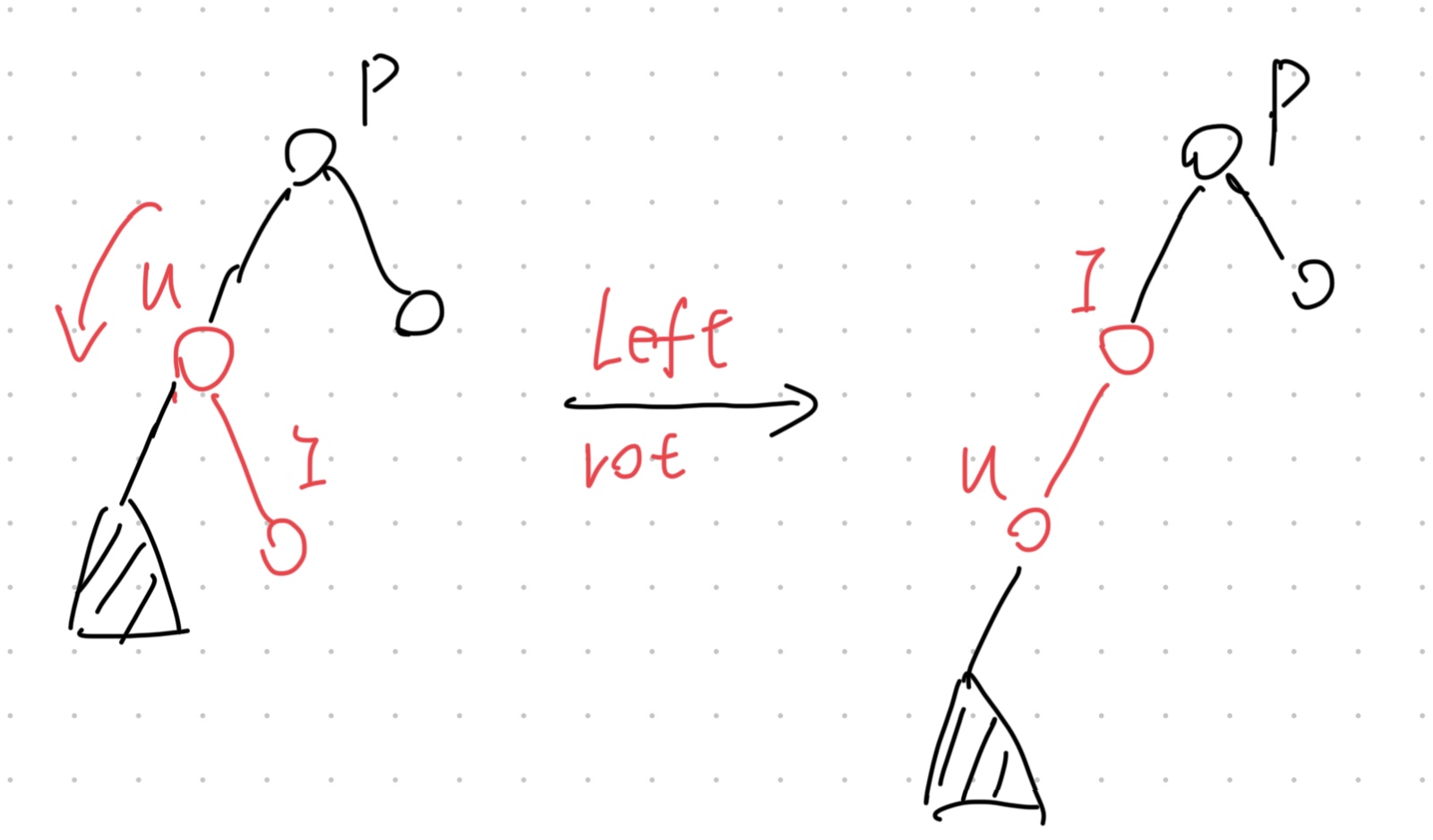
- 1.Perform a Left Rotation on the parent $u$ to turn it into the case 2-2-1.
- 2.Follow the case 2-2-1 process.
This case takes $O(1)$ time.
Deletion Operations
- 1.Delete as BST, which takes $O(log n)$ time.
- 2.Restore the balance property of the RBT, which takes $O(log n)$ time.
Deleted node has at most one child,exclude NULL.
Restore After Deletion
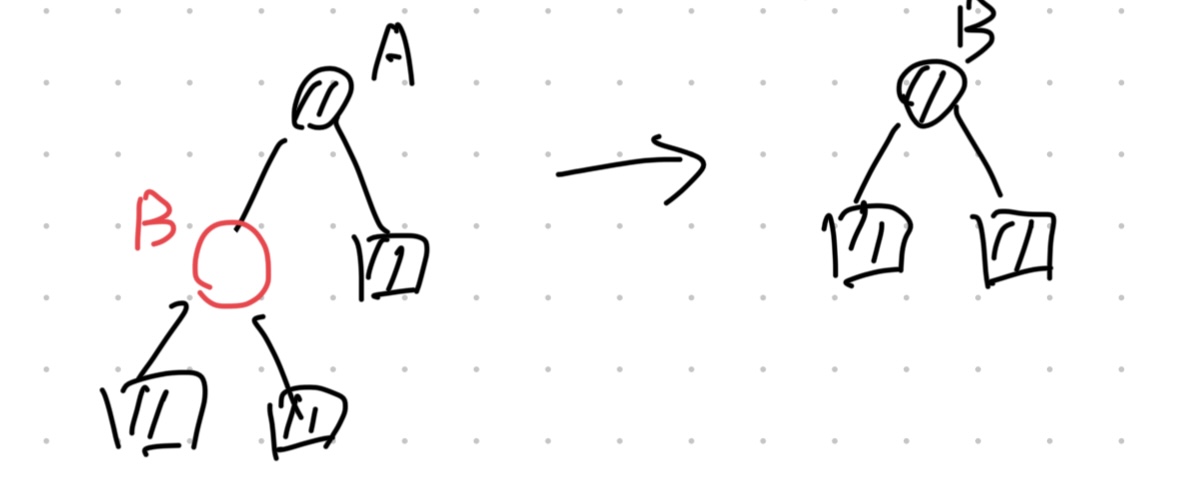
case 1: The deleted node is red

- For the case in the above of the picture, it is impossible because the tree rooted at $A$ is not balanced before deletion.
- For the case in the below of the picture, it is okay and we only need to delete $A$ and replace it with a NULL node.
This case takes $O(1)$ time.
case 2: The deleted node is black
case 2-1: the deleted node has red children
- As Lemma 1 shows, the deledted node has at most one child,exclude NULL.
- If the deleted node has a red child, it can only be the situation like the above picture.
- We first delete $A$ and replace it with its child $B$.
- Then we color $B$ black and the balance property of the RBT is restored.
This case takes $O(1)$ time.
case 2-2: the deleted node has black children
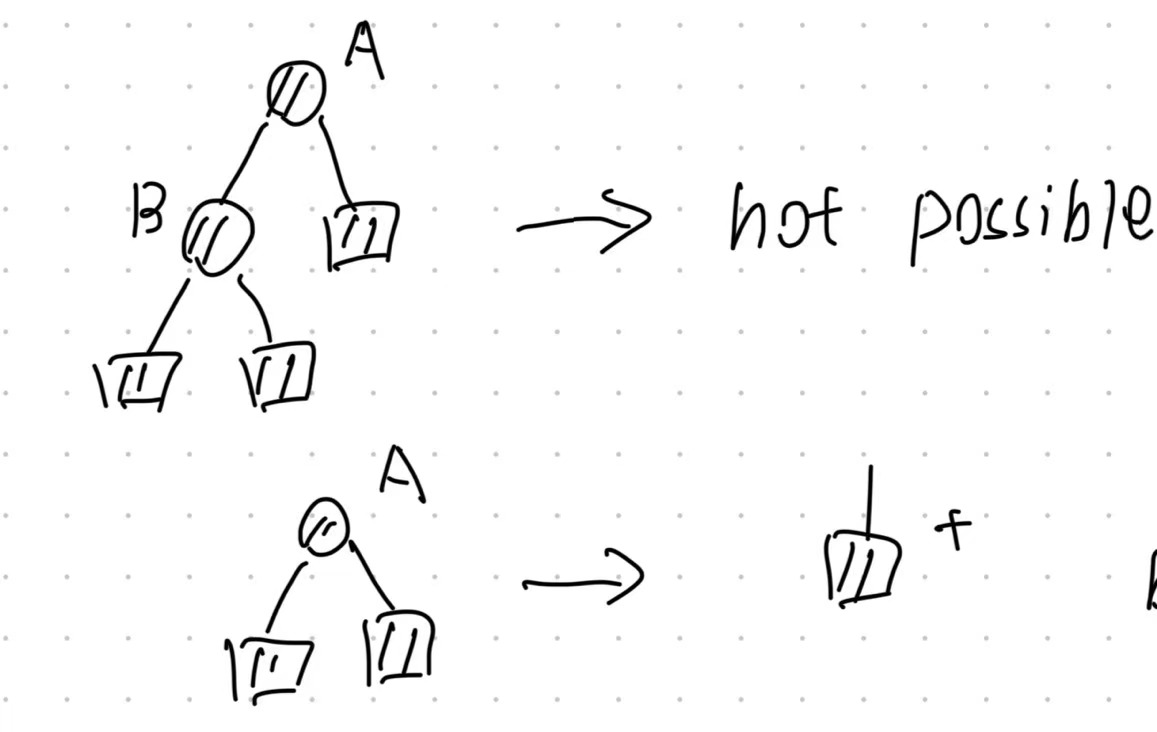
- For the case in the above of the picture, it is impossible because the tree rooted at $A$ is not balanced before deletion(The subtrees of $A$ have different black-heights).
- For the case in the below of the picture, it is okay and we first delete $A$ and replace it with a simple NULL node?
- If we only replace $A$ with a NULL node, the balance property of the RBT will not be restored due to the changes of the black-heights of the Tree.
- To simplify the problem, we just mark the NULL node as Black-Plus,so that the black-height of the Tree is not changed.And we remove the BP node later.
This case takes $O(logn)$ time due to the Remove BP node operation.
Remove BP node operation
case 1:
- Path $p$-$u$-$s$ is in one direction
- $u$, the sibling of BP node, is black
- $s$, son of $u$, is red.
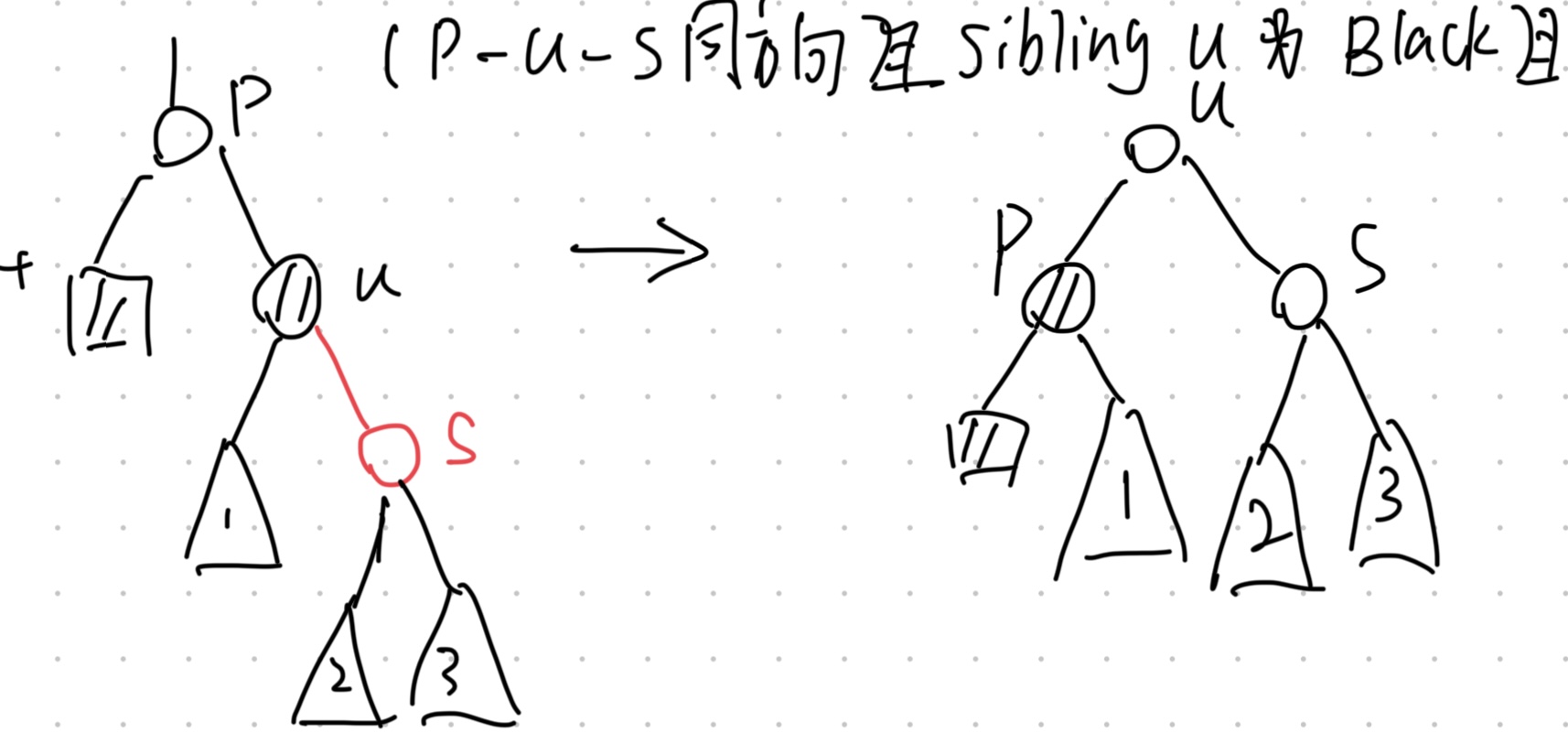
- 1.Perform a Left Rotation on $u$.
- 2.Remove the BP mark.
This case takes $O(1)$ time.
case 2:
- Path $p$-$u$-$s$ is in the different direction
- $u$, the sibling of BP node, is black
- $s$, son of $u$, is red.
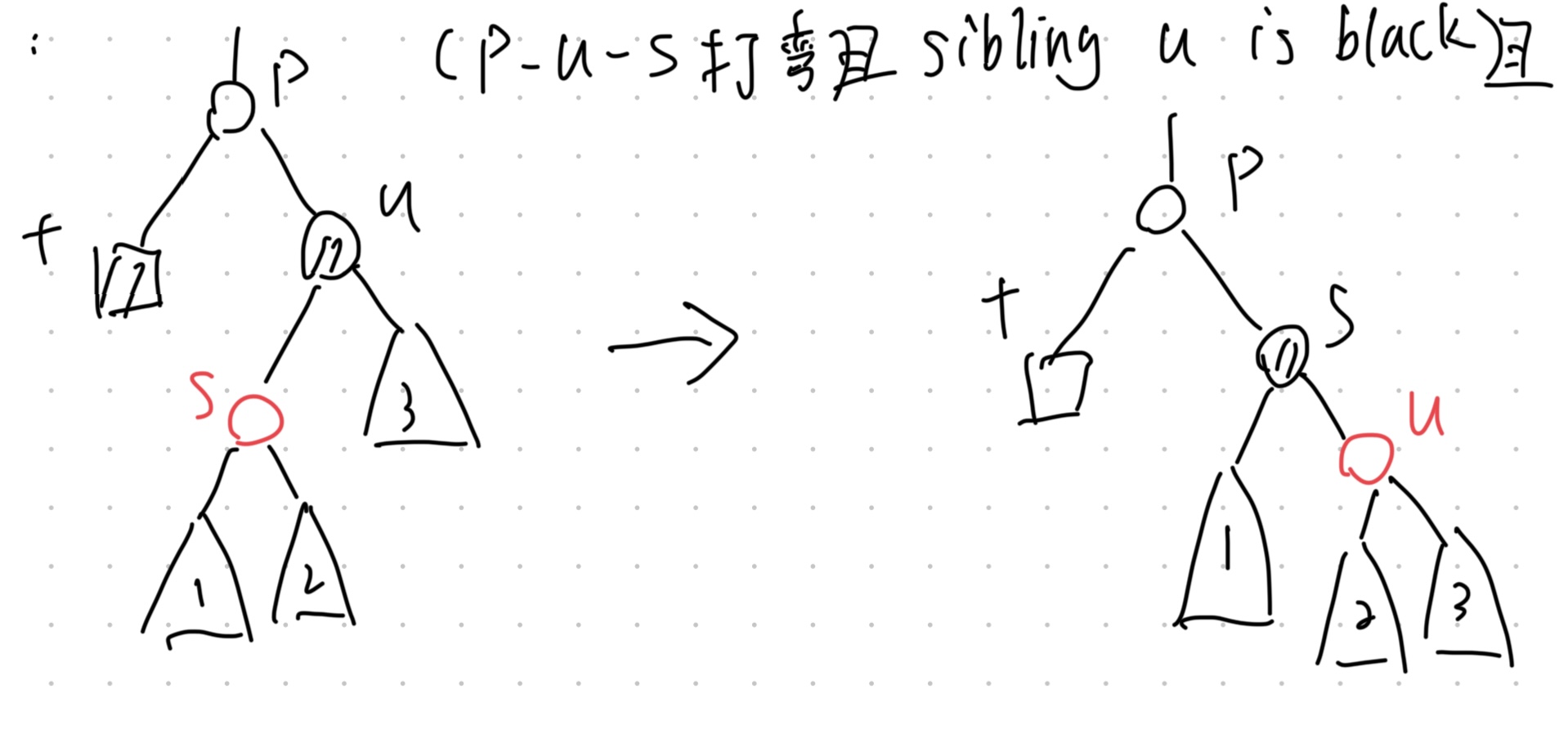
- 1.Perform a Right Rotation on $s$.
- 2.Color $s$ black and $u$ red.
- 3.The case 2 turns into the case 1.
- 4.Remove as case 1.
This case takes $O(1)$ time.
case 3:
- $u$, the sibling of BP node, is black
- $s$, son of $u$, is black.
case 3-1:
- $p$, the parent of BP node, is red.
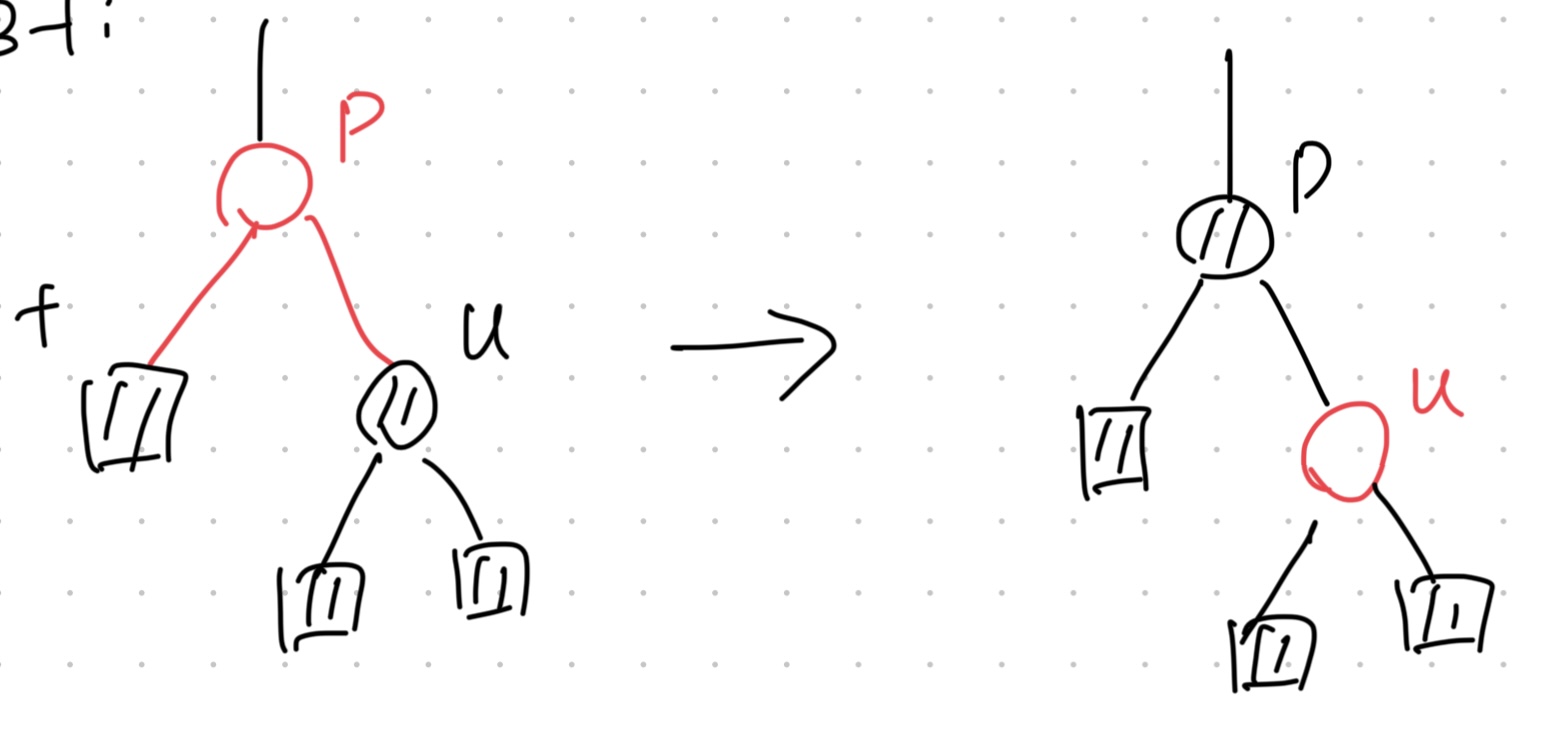
- 1.Color $p$ black.
- 2.Color $u$ red.
- 3.Remove the BP mark.
This case takes $O(1)$ time.
case 3-2:
- $p$, the parent of BP node, is black.
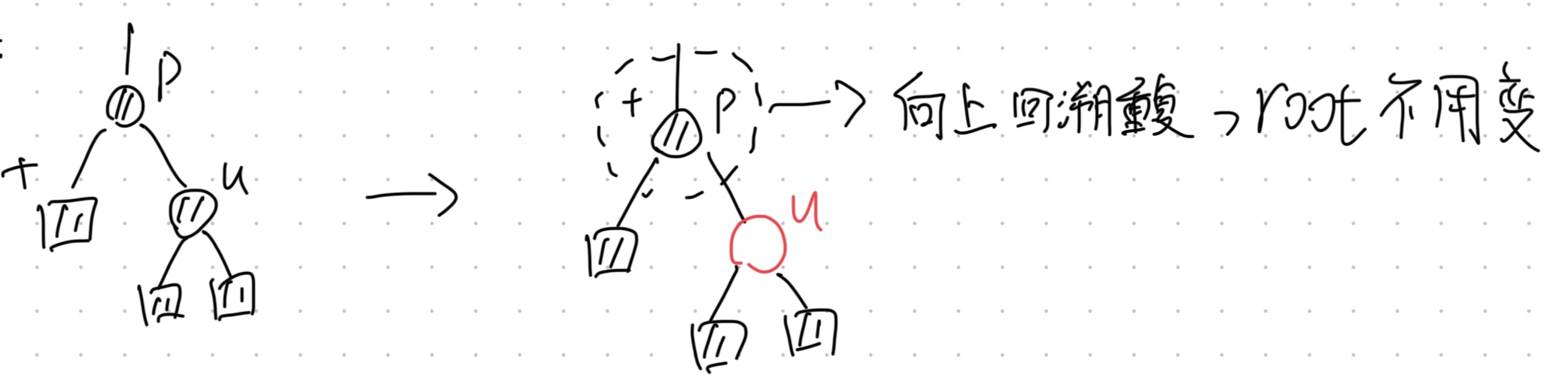
- 1.Mark $p$ as BP node.
- 2.Color $u$ red.
- 3.Remove the BP mark.
- 4.Continue the case 3-2 process until $p$ is red or $p$ is the root.
- 5.If $p$ is red, continue the case 3-1 process.
- 6.If $p$ is the root, do as case 3-2 and ignore the first step.
This case takes $O(logn)$ time.
case 4:
- $u$, the sibling of BP node, is red.
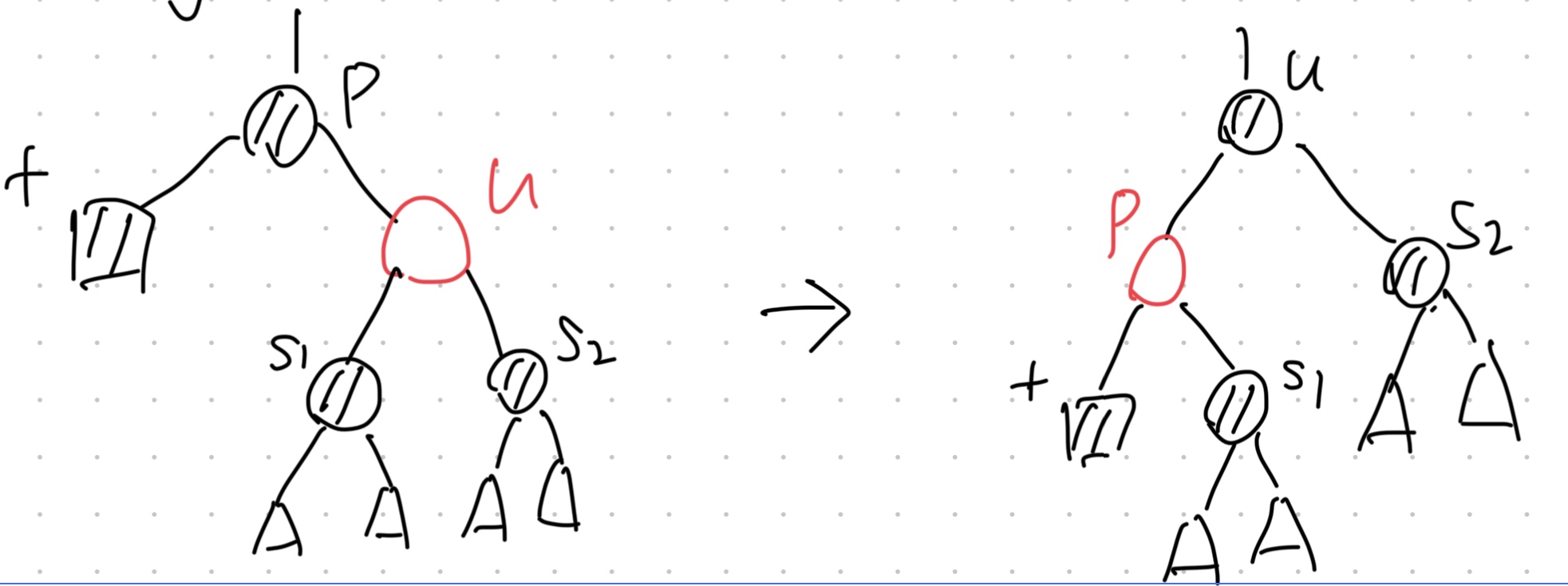
- 1.Perform a Left Rotation on $u$.
- 2.Color $u$ black.
- 3.Color $p$ red.
- 4.This operation turns the case into other cases depending on the real condition.
- 5.Then follow the corresponding case to remove the BP node.
This case takes $O(logn)$ time.
Summary
Time Complexity
| AVL Tree | Red-Black Tree | |
|---|---|---|
| Insert | $O(logn)$ | $O(logn)$ |
| Delete | $O(logn)$ | $O(logn)$ |
| Restore | $O(1)$ | $O(logn)$ |
| Remove BP node | NULL | $O(logn)$ |
Number of Rotations
| AVL Tree | Red-Black Tree | |
|---|---|---|
| Insert | $\leq 2$ | $\leq 2$ |
| Delete | $O(\log n)$ | $\leq 3$ |
